
| A. | -1 | B. | 0 | C. | 2 | D. | 3 |
分析 数列{an}是以$\frac{1}{2}$为公差的等差数列,可得an=a1+$\frac{1}{2}$(n-1),Sn=b1+b2+…+bn=2sin(πa1+φ)+$2sin(π{a}_{1}+\frac{π}{2}+φ)$+…+2sin$(π{a}_{1}+\frac{n-1}{2}π+φ)$,φ∈(0,$\frac{π}{2}$),S4=0.利用其周期性即可得出.
解答 解:数列{an}是以$\frac{1}{2}$为公差的等差数列,∴an=a1+$\frac{1}{2}$(n-1),
∵bn=2sin(πan+φ)=2sin$(π{a}_{1}+\frac{n-1}{2}π+φ)$,φ∈(0,$\frac{π}{2}$),
∴Sn=b1+b2+…+bn=2sin(πa1+φ)+$2sin(π{a}_{1}+\frac{π}{2}+φ)$+…+2sin$(π{a}_{1}+\frac{n-1}{2}π+φ)$,φ∈(0,$\frac{π}{2}$),
∴S4=0.
∴S4n+1=S1∈[-2,2],S4n+2=S2=2$\sqrt{2}$sin(πa1+φ)∈[-2$\sqrt{2}$,2$\sqrt{2}$],S4n+3=S3=2cos(πa1+φ)∈[-2,2],S4n+4=S4=0.
则Sn不可能是3.
故选:D.
点评 本题考查了等差数列的通项公式、诱导公式、和差公式、三角函数的周期性,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
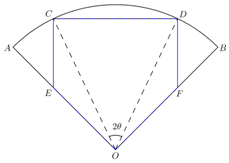 现有半径为R、圆心角(∠AOB)为90°的扇形材料,要裁剪出一个五边形工件OECDF,如图所示.其中E,F分别在OA,OB上,C,D在$\widehat{AB}$上,且OE=OF,EC=FD,∠ECD=∠CDF=90°.记∠COD=2θ,五边形OECDF的面积为S.
现有半径为R、圆心角(∠AOB)为90°的扇形材料,要裁剪出一个五边形工件OECDF,如图所示.其中E,F分别在OA,OB上,C,D在$\widehat{AB}$上,且OE=OF,EC=FD,∠ECD=∠CDF=90°.记∠COD=2θ,五边形OECDF的面积为S.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{3}{8}$ | C. | $\frac{8}{27}$ | D. | $\frac{12}{27}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{2}{3}$) | B. | [$\frac{1}{3}$,$\frac{2}{3}$) | C. | ($\frac{1}{2}$,+∞) | D. | [$\frac{1}{2}$,$\frac{2}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a⊥b,a⊥α,b?α,则b∥α | B. | 若a⊥b,a⊥α,b⊥β,则α⊥β | ||
| C. | 若a⊥β,α⊥β,则a∥α或a?α | D. | 若a∥α,α⊥β,则a⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | .16或36 | B. | 36或64 | C. | 16或64 | D. | 36 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com