

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
人数 | 10 | 15 | 20 | 25 | 30 | 35 | 40 |
件数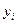 | 4 | 7 | 12 | 15 | 20 | 23 | 27 |
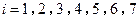 .
. (Ⅱ)求回归直线方程.(结果保留到小数点后两位)
(Ⅱ)求回归直线方程.(结果保留到小数点后两位) ,
, ,
,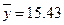 ,
,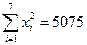 ,
, ,
,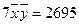 )
)
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.5 | B.4 | C.7 | D.6 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 参考数据 | 当 ≤2.706时,无充分证据判定变量A,B有关,可以认为两变量无关; ≤2.706时,无充分证据判定变量A,B有关,可以认为两变量无关; |
当 >2.706时,有90%把握判定变量A,B有关; >2.706时,有90%把握判定变量A,B有关; | |
当 >3.841时,有95%把握判定变量A,B有关; >3.841时,有95%把握判定变量A,B有关; | |
当 >6. >6. 635时,有99%把握判定变量A,B有关。 635时,有99%把握判定变量A,B有关。 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 下表是
下表是 部分统计数据:
部分统计数据:
| 年份 | 2002 | 2004 | 2006 | 2008 | 2010 |
| 需求量(万吨) | 236 | 246 | 257 | 276 | 286 |
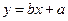 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 的号码为16,则第四组抽取的号码
的号码为16,则第四组抽取的号码 为___________________.
为___________________.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
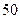 名学生。调査结果表明:在爱看课外书的
名学生。调査结果表明:在爱看课外书的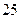 人中有
人中有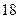 人作文水平好,另
人作文水平好,另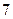 人作文水平一般;在不爱看课外书的
人作文水平一般;在不爱看课外书的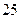 人中有
人中有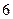 人作文水平好,另
人作文水平好,另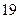 人作文水平一般.
人作文水平一般.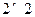 列联表,并运用独立性检验思想,指出有多大把握认为中学生的作文
列联表,并运用独立性检验思想,指出有多大把握认为中学生的作文 水平与爱看课外书有关系?
水平与爱看课外书有关系?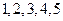 ,某
,某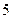 名爱看
名爱看 课外书且作文水平一般的学生也分别编号为
课外书且作文水平一般的学生也分别编号为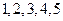 ,从这两组学生中各任选
,从这两组学生中各任选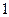 人进行学习交流,求被选取的两名学生的编号之和为
人进行学习交流,求被选取的两名学生的编号之和为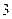 的倍数或
的倍数或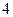 的倍数的概率.
的倍数的概率.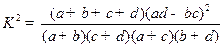
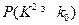 | 0. 10 | 0. 05 | 0. 025 | 0.010 | 0. 005 | 0. 001 |
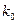 | 2. 706 | 3. 841 | 5. 024 | 6. 635 | 7. 879 | 10. 828 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
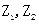 满足
满足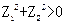 ,则
,则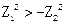 ;
; 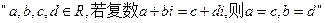 类比推出
类比推出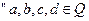 ,若
,若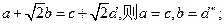
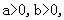 则
则 ; (4)线性回归方程
; (4)线性回归方程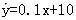 中,当变量x平均增加一个单
中,当变量x平均增加一个单 位
位 时,
时,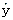 平均增加0.1个单位。 其中一定正确的语句是 (填序号)。
平均增加0.1个单位。 其中一定正确的语句是 (填序号)。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com