
【题目】改革开放以来,中国快递行业持续快速发展,快递业务量从上世纪![]() 年代的
年代的![]() 万件提升到2018年的
万件提升到2018年的![]() 亿件,快递行业的发展也给我们的生活带来了很大便利.已知某市某快递点的收费标准为:首重(重量小于等于
亿件,快递行业的发展也给我们的生活带来了很大便利.已知某市某快递点的收费标准为:首重(重量小于等于![]() )收费
)收费![]() 元,续重
元,续重![]() 元
元![]() (不足
(不足![]() 按
按![]() 算). (如:一个包裹重量为
算). (如:一个包裹重量为![]() 则需支付首付
则需支付首付![]() 元,续重
元,续重![]() 元,一共
元,一共![]() 元快递费用)
元快递费用)
(1)若你有三件礼物![]() 重量分别为
重量分别为![]() ,要将三个礼物分成两个包裹寄出(如:
,要将三个礼物分成两个包裹寄出(如:![]() 合为一个包裹,
合为一个包裹,![]() 一个包裹),那么如何分配礼物,使得你花费的快递费最少?
一个包裹),那么如何分配礼物,使得你花费的快递费最少?
(2)为了解该快递点2019年的揽件情况,在2019年内随机抽查了![]() 天的日揽收包裹数(单位:件),得到如下表格:
天的日揽收包裹数(单位:件),得到如下表格:
包裹数(单位:件) |
|
|
|
|
天数(天) |
|
|
|
|
现用这![]() 天的日揽收包裹数估计该快递点2019年的日揽收包裏数.若从2019年任取
天的日揽收包裹数估计该快递点2019年的日揽收包裏数.若从2019年任取![]() 天,记这
天,记这![]() 天中日揽收包裹数超过
天中日揽收包裹数超过![]() 件的天数为随机变量
件的天数为随机变量![]() 求
求![]() 的分布列和期望
的分布列和期望
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:高中数学 来源: 题型:
【题目】为研究![]() 因子对某物种繁殖的影响,某生物研究所开展了系列研究,研究过程中,选取了生长状况相同的三组样本分别标记为
因子对某物种繁殖的影响,某生物研究所开展了系列研究,研究过程中,选取了生长状况相同的三组样本分别标记为![]() 组,
组,![]() 组,
组,![]() 组进行繁殖实验,已知每组均繁殖10个个体,其中
组进行繁殖实验,已知每组均繁殖10个个体,其中![]() 组正常培养,
组正常培养,![]() 组,
组,![]() 组均在食物中添加
组均在食物中添加![]() 因子,一个月后统计存活率,已知
因子,一个月后统计存活率,已知![]() 组存活7个个体,
组存活7个个体,![]() 组存活8个个体,
组存活8个个体,![]() 组存活5个个体,现将这20个存活个体集中,并从中任取3个个体
组存活5个个体,现将这20个存活个体集中,并从中任取3个个体
(1)求抽取的3个存活个体中有来自同一组的概率
(2)记![]() 为所抽取的3个个体中来自
为所抽取的3个个体中来自![]() 组的个体的数量,求
组的个体的数量,求![]() 的分布列和数学期望
的分布列和数学期望
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人2018年的家庭总收人为![]() 元,各种用途占比如图中的折线图,
元,各种用途占比如图中的折线图,![]() 年家庭总收入的各种用途占比统计如图中的条形图,已知
年家庭总收入的各种用途占比统计如图中的条形图,已知![]() 年的就医费用比
年的就医费用比![]() 年的就医费用增加了
年的就医费用增加了![]() 元,则该人
元,则该人![]() 年的储畜费用为( )
年的储畜费用为( )

A.![]() 元B.
元B.![]() 元C.
元C.![]() 元D.
元D.![]() 元
元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆台![]() 的轴截面为等腰梯形
的轴截面为等腰梯形![]() ,
,![]() 圆台
圆台![]() 的侧面积为
的侧面积为![]() .若点
.若点![]() 分别为圆
分别为圆![]() 上的动点,且点
上的动点,且点![]() 在平面
在平面![]() 的同侧.
的同侧.

(1)求证:![]() ;
;
(2)若![]() ,则当三棱锥
,则当三棱锥![]() 的体积取最大值时,求
的体积取最大值时,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,椭圆C:![]() (
(![]() )的离心率为
)的离心率为![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,
,![]() ,椭圆C过点
,椭圆C过点![]() ,T为直线
,T为直线![]() 上的动点,过点T作椭圆C的切线
上的动点,过点T作椭圆C的切线![]() ,
,![]() ,A,B为切点.
,A,B为切点.
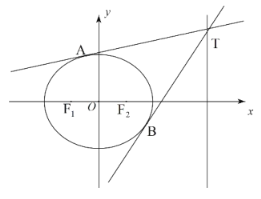
(1)求证:A,![]() ,B三点共线;
,B三点共线;
(2)过点![]() 作一条直线与曲线C交于P,Q两点.过P,Q作直线
作一条直线与曲线C交于P,Q两点.过P,Q作直线![]() 的垂线,垂足依次为M,N.求证:直线
的垂线,垂足依次为M,N.求证:直线![]() 与
与![]() 交于定点.
交于定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com