
已知函数y=a![]() (a>0,且a≠1),当x∈[1,3]时有最小值8,求a的值.
(a>0,且a≠1),当x∈[1,3]时有最小值8,求a的值.
|
分析:y=a 解:令u=x2-3x+3,则y=au,u= 由x∈[1,3],知umin=u 所以,当a>1时,ymin=a 当0<a<1时,ymin=a3=8,解得a=2(舍去). 因此,a的值为16. 点评:求复合函数的值域,往往使用换元法将复合函数分解为两个或两个以上的基本初等函数,然后由其定义域确定中间变量u的值域,再以u为自变量确定y的值域,这种方法是确定复合函数值域的一般方法. 求解函数最值的方法比较多,而求解指、对、幂函数最值的常用方法是以上四种方法.需要注意的是,有时对同一道题并不只用一种方法就能解决,往往需要同时利用多种方法求解,如换元法、分类讨论法等往往贯穿于其他的方法中. |


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源:高考零距离 二轮冲刺优化讲练 数学 题型:044
| |||||||||||
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)的定义域为[-1,5],部分对应值如下表.f(x)的导函数y=f′(x)的图象如图所示.
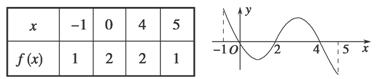
下列关于函数f(x)的命题:
①函数y=f(x)是周期函数;
②函数f(x)在[0,2]上是减函数;
③如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最大值为4;
④当1<a<2时,函数y=f(x)-a有4个零点.
其中真命题的个数有 ( ).
A.4 B.3 C.2 D.1
查看答案和解析>>
科目:高中数学 来源:2013-2014学年上海交大附中高三数学理总复习二等差数列、等比数列练习卷(解析版) 题型:选择题
已知函数y=anx2(an≠0,n∈N*)的图像在x=1处的切线斜率为2an-1+1(n≥2,n∈N*),且当n=1时其图像过点(2,8),则a7的值为( )
A. B.7
B.7
C.5 D.6
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西省高三10月月考理科数学 题型:选择题
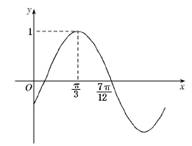
已知函数y=sin(ωx+φ)的部分图象如图所( )
A.ω=1,φ=
B.ω=1,φ=-
C.ω=2,φ=
D.ω=2,φ=-
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com