
【题目】已知函数f(x)=x3+3|x﹣a|(a∈R).
(1)若f(x)在[﹣1,1]上的最大值和最小值分别记为M(a),m(a),求M(a)﹣m(a);
(2)设b∈R,若[f(x)+b]2≤4对x∈[﹣1,1]恒成立,求3a+b的取值范围.
【答案】
(1)解:∵f(x)=x3+3|x﹣a|= ![]() ,
,
∴f′(x)= ![]() ,
,
①a≤﹣1时,∵﹣1≤x≤1,∴x≥a,f(x)在(﹣1,1)上是增函数,
∴M(a)=f(1)=4﹣3a,m(a)=f(﹣1)=﹣4﹣3a,
∴M(a)﹣m(a)=8;
②﹣1<a<1时,x∈(a,1),f(x)=x3+3x﹣3a,在(a,1)上是增函数;x∈(﹣1,a),f(x)=x3﹣3x+3a,在(﹣1,a)上是减函数,
∴M(a)=max{f(1),f(﹣1)},m(a)=f(a)=a3,
∵f(1)﹣f(﹣1)=﹣6a+2,
∴﹣1<a≤ ![]() 时,M(a)﹣m(a)=﹣a3﹣3a+4;
时,M(a)﹣m(a)=﹣a3﹣3a+4;
![]() <a<1时,M(a)﹣m(a)=﹣a3+3a+2;
<a<1时,M(a)﹣m(a)=﹣a3+3a+2;
③a≥1时,有x≤a,f(x)在(﹣1,1)上是减函数,
∴M(a)=f(﹣1)=2+3a,m(a)=f(1)=﹣2+3a,
∴M(a)﹣m(a)=4;
(2)解:令h(x)=f(x)+b,则h(x)= ![]() ,h′(x)=
,h′(x)= ![]() ,
,
∵[f(x)+b]2≤4对x∈[﹣1,1]恒成立,
∴﹣2≤h(x)≤2对x∈[﹣1,1]恒成立,
由(Ⅰ)知,
①a≤﹣1时,h(x)在(﹣1,1)上是增函数,最大值h(1)=4﹣3a+b,最小值h(﹣1)=﹣4﹣3a+b,则﹣4﹣3a+b≥﹣2且4﹣3a+b≤2矛盾;
②﹣1<a≤ ![]() 时,最小值h(a)=a3+b,最大值h(1)=4﹣3a+b,∴a3+b≥﹣2且4﹣3a+b≤2,
时,最小值h(a)=a3+b,最大值h(1)=4﹣3a+b,∴a3+b≥﹣2且4﹣3a+b≤2,
令t(a)=﹣2﹣a3+3a,则t′(a)=3﹣3a2>0,t(a)在(0, ![]() )上是增函数,∴t(a)>t(0)=﹣2,
)上是增函数,∴t(a)>t(0)=﹣2,
∴﹣2≤3a+b≤0;
③ ![]() <a<1时,最小值h(a)=a3+b,最大值h(﹣1)=3a+b+2,则a3+b≥﹣2且3a+b+2≤2,∴﹣
<a<1时,最小值h(a)=a3+b,最大值h(﹣1)=3a+b+2,则a3+b≥﹣2且3a+b+2≤2,∴﹣ ![]() <3a+b≤0;
<3a+b≤0;
④a≥1时,最大值h(﹣1)=3a+b+2,最小值h(1)=3a+b﹣2,则3a+b﹣2≥﹣2且3a+b+2≤2,∴3a+b=0.
综上,3a+b的取值范围是﹣2≤3a+b≤0
【解析】(1)利用分段函数,结合[﹣1,1],分类讨论,即可求M(a)﹣m(a);(2)令h(x)=f(x)+b,则h(x)= ![]() ,h′(x)=
,h′(x)= ![]() ,则[f(x)+b]2≤4对x∈[﹣1,1]恒成立,转化为﹣2≤h(x)≤2对x∈[﹣1,1]恒成立,分类讨论,即可求3a+b的取值范围.
,则[f(x)+b]2≤4对x∈[﹣1,1]恒成立,转化为﹣2≤h(x)≤2对x∈[﹣1,1]恒成立,分类讨论,即可求3a+b的取值范围.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:
【题目】给出下列类比推理命题(其中![]() 为有理数集,
为有理数集,![]() 为实数集,
为实数集,![]() 为复数集),其中类比结论正确的是( )
为复数集),其中类比结论正确的是( )
A. “若![]() ,则
,则![]() ”类比推出“若
”类比推出“若![]() ,则
,则![]() ”.
”.
B. ![]() 类比推出
类比推出![]()
C. ![]() 类比推出
类比推出![]()
D. “若![]() ,则
,则![]() ”类比推出“若
”类比推出“若![]() ,则
,则![]() ”.
”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a1=1,an+1= ![]() +b(n∈N*)
+b(n∈N*)
(1)若b=1,求a2 , a3及数列{an}的通项公式;
(2)若b=﹣1,问:是否存在实数c使得a2n<c<a2n+1对所有的n∈N*成立,证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某人在垂直于水平地面ABC的墙面前的点A处进行射击训练.已知点A到墙面的距离为AB,某目标点P沿墙面上的射线CM移动,此人为了准确瞄准目标点P,需计算由点A观察点P的仰角θ的大小.若AB=15m,AC=25m,∠BCM=30°,则tanθ的最大值是 . (仰角θ为直线AP与平面ABC所成角) 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第一届“一带一路”国际合作高峰论坛于2017年5月14日至15日在北京举行,这是2017年我国重要的主场外交活动,对推动国际和地区合作具有重要意义.某高中政教处为了调查学生对“一带一路”的关注情况,在全校组织了“一带一路知多少”的知识问卷测试,并从中随机抽取了12份问卷,得到其测试成绩(百分制),如茎叶图所示.
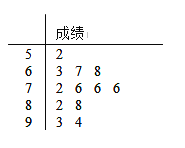
(1)写出该样本的众数、中位数,若该校共有3000名学生,试估计该校测试成绩在70分以上的人数;
(2)从所抽取的70分以上的学生中再随机选取4人.
①记![]() 表示选取4人的成绩的平均数,求
表示选取4人的成绩的平均数,求![]() ;
;
②记![]() 表示测试成绩在80分以上的人数,求
表示测试成绩在80分以上的人数,求![]() 的分布和数学期望.
的分布和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列推理是类比推理的是( )
A. 由周期函数的定义判断某函数是否为周期函数
B. 由![]() ,猜想任何一个小6的偶数都是两个奇质数之和
,猜想任何一个小6的偶数都是两个奇质数之和
C. 平面内不共线的3个点确定一个圆,由此猜想空间不共面的4个点确定一个球
D. 已知![]() 为定点,若动点P满足
为定点,若动点P满足![]() (其中
(其中![]() 为常数),则点
为常数),则点![]() 的轨迹为椭圆
的轨迹为椭圆
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】改革开放四十周年纪念币从2018年12月5日起可以开始预约![]() 通过市场调查,得到该纪念章每1枚的市场价
通过市场调查,得到该纪念章每1枚的市场价![]() 单位:元
单位:元![]() 与上市时间
与上市时间![]() 单位:天
单位:天![]() 的数据如下:
的数据如下:
上市时间x天 | 8 | 10 | 32 |
市场价y元 | 82 | 60 | 82 |
![]() 根据上表数据,从下列函数:
根据上表数据,从下列函数:![]() ;
;![]() ;
;![]() 中选取一个恰当的函数刻画改革开放四十周年纪念章的市场价y与上市时间x的变化关系并说明理由
中选取一个恰当的函数刻画改革开放四十周年纪念章的市场价y与上市时间x的变化关系并说明理由
![]() 利用你选取的函数,求改革开放四十周年纪念章市场价最低时的上市天数及最低的价格.
利用你选取的函数,求改革开放四十周年纪念章市场价最低时的上市天数及最低的价格.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经统计某射击运动员随机命中的概率可视为![]() ,为估计该运动员射击4次恰好命中3次的概率,现采用随机模拟的方法,先由计算机产生0到9之间取整数的随机数,用0,1,2 没有击中,用3,4,5,6,7,8,9 表示击中,以 4个随机数为一组, 代表射击4次的结果,经随机模拟产生了20组随机数:
,为估计该运动员射击4次恰好命中3次的概率,现采用随机模拟的方法,先由计算机产生0到9之间取整数的随机数,用0,1,2 没有击中,用3,4,5,6,7,8,9 表示击中,以 4个随机数为一组, 代表射击4次的结果,经随机模拟产生了20组随机数:
7525,0293,7140,9857,0347,4373,8638,7815,1417,5550
0371,6233,2616,8045,6011,3661,9597,7424,7610,4281
根据以上数据,则可估计该运动员射击4次恰好命中3次的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com