
【题目】如甲图所示,在矩形ABCD中,AB=4,AD=2,E是CD的中点,将△ADE沿AE折起到△D1AE位置,使平面D1AE⊥平面ABCE,得到乙图所示的四棱锥D1﹣ABCE.
(Ⅰ)求证:BE⊥平面D1AE;
(Ⅱ)求二面角A﹣D1E﹣C的余弦值.
【答案】证明:(Ⅰ)如图,取AE中点F,连D1F, 在△AD1E中,∵D1A=D1E=2,∴D1F⊥AE,
又∵平面D1AE⊥平面ABCE,∴D1F⊥平面ABCE,
∵BE平面ABCE,∴D1F⊥BE.
在△ABE中,可得 ![]() ,BE=2
,BE=2 ![]() ,AB=4,
,AB=4,
∴BE⊥AE,又∵D1F∩AE=F,
∴BE⊥平面D1AE;
(Ⅱ)解:由题意,取AB中点G,以E为坐标原点,分别以EG,EC为x,y轴正方向建立空间直角坐标系E﹣xyz.
如图所示,则E(0,0,0),C(0,2,0)D1(1,﹣1, ![]() ),B(2,2,0),
),B(2,2,0),
由(Ⅰ)知: ![]() 是平面AD1E的法向量,
是平面AD1E的法向量,
设平面CED1的法向量为 ![]() ,则
,则 ,令z=1,则x=﹣
,令z=1,则x=﹣ ![]() ,y=0,
,y=0,
∴ ![]() ,
,
设二面角A﹣D1E﹣C的平面角为θ,
则|cosθ|=|cos< ![]() >|=|
>|=| ![]() |=
|= ![]() .
.
由图可知,二面角A﹣D1E﹣C的平面角为钝角,
∴cos ![]() ,
,
即二面角A﹣D1E﹣C的余弦值为 ![]() .
.
【解析】(Ⅰ)取AE中点F,连D1F,求解三角形可得D1F⊥AE,又平面D1AE⊥平面ABCE,利用面面垂直的性质可得D1F⊥平面ABCE,从而得到D1F⊥BE.在△ABE中,可得BE⊥AE,再利用线面垂直的判定可得BE⊥平面D1AE;(Ⅱ)由题意,取AB中点G,以E为坐标原点,分别以EG,EC为x,y轴正方向建立空间直角坐标系E﹣xyz.求出所用点的坐标,得到平面AD1E与平面CED1的法向量.利用两法向量所成角的余弦值可得二面角A﹣D1E﹣C的余弦值.
【考点精析】通过灵活运用直线与平面垂直的判定,掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想即可以解答此题.


科目:高中数学 来源: 题型:
【题目】已知曲线C1的极坐标方程为ρ=6cosθ,曲线C2的极坐标方程为θ= ![]() (p∈R),曲线C1 , C2相交于A,B两点. (Ⅰ)把曲线C1 , C2的极坐标方程转化为直角坐标方程;
(p∈R),曲线C1 , C2相交于A,B两点. (Ⅰ)把曲线C1 , C2的极坐标方程转化为直角坐标方程;
(Ⅱ)求弦AB的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的各项都是正数,它的前n项和为Sn , 满足2Sn=an2+an , 记bn=(﹣1)n ![]() .
.
(1)求数列{an}的通项公式;
(2)求数列{bn}的前2016项的和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x2+aln(x+1),a∈R.
(Ⅰ)讨论函数f(x)的单调性;
(Ⅱ)若函数f(x)有两个极值点x1 , x2 , 且x1<x2 , 求证:f(x2)≥( ![]() ﹣1)x2 .
﹣1)x2 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=m﹣|x﹣2|,m∈R,且f(x+2)≥0的解集为[﹣3,3].
(Ⅰ)解不等式:f(x)+f(x+2)>0;
(Ⅱ)若a,b,c均为正实数,且满足a+b+c=m,求证: ![]() ≥3.
≥3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有以下命题:
①若函数f(x)既是奇函数又是偶函数,则f(x)的值域为{0};
②若函数f(x)是偶函数,则f(|x|)=f(x);
③若函数f(x)在其定义域内不是单调函数,则f(x)不存在反函数;
④若函数f(x)存在反函数f﹣1(x),且f﹣1(x)与f(x)不完全相同,则f(x)与f﹣1(x)图象的公共点必在直线y=x上;
其中真命题的序号是 . (写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AB∥DC,AD=AB=BC=1, ![]() ,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=1,点M在线段EF上.
,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=1,点M在线段EF上. 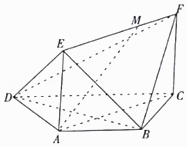
(1)当 ![]() 为何值时,AM∥平面BDF?证明你的结论;
为何值时,AM∥平面BDF?证明你的结论;
(2)求二面角B﹣EF﹣D的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=sin(2x﹣ ![]() )的图象向左平移
)的图象向左平移 ![]() 个单位后,得到y=g(x)的图象,则下列说法错误的是( )
个单位后,得到y=g(x)的图象,则下列说法错误的是( )
A.y=g(x)的最小正周期为π
B.y=g(x)的图象关于直线x= ![]() 对称
对称
C.y=g(x)在[﹣ ![]() ,
, ![]() ]上单调递增
]上单调递增
D.y=g(x)的图象关于点( ![]() ,0)对称
,0)对称
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com