
某市为控制大气PM2.5的浓度,环境部门规定:该市每年的大气主要污染物排放总量不能超过55万吨,否则将采取紧急限排措施.已知该市2013年的大气主要污染物排放总量为40万吨,通过技术改造和倡导绿色低碳生活等措施,此后每年的原大气主要污染物排放最比上一年的排放总量减少10%.同时,因为经济发展和人口增加等因素,每年又新增加大气主要污染物排放量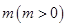 万吨.
万吨.
(1)从2014年起,该市每年大气主要污染物排放总量(万吨)依次构成数列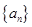 ,求相邻两年主要污染物排放总量的关系式;
,求相邻两年主要污染物排放总量的关系式;
(2)证明:数列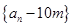 是等比数列;
是等比数列;
(3)若该市始终不需要采取紧急限排措施,求m的取值范围.
 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:解答题
若正项数列 满足条件:存在正整数
满足条件:存在正整数 ,使得
,使得 对一切
对一切 都成立,则称数列
都成立,则称数列 为
为 级等比数列.
级等比数列.
(1)已知数列 为2级等比数列,且前四项分别为
为2级等比数列,且前四项分别为 ,求
,求 的值;
的值;
(2)若 为常数),且
为常数),且 是
是 级等比数列,求
级等比数列,求 所有可能值的集合,并求
所有可能值的集合,并求 取最小正值时数列
取最小正值时数列 的前
的前 项和
项和 ;
;
(3)证明: 为等比数列的充要条件是
为等比数列的充要条件是 既为
既为 级等比数列,
级等比数列, 也为
也为 级等比数列.
级等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知数列{ }中,
}中, 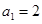 ,
,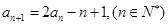 ,
,
(1)求证数列{
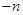 }为等比数列.
}为等比数列.
(2)判断265是否是数列{ }中的项,若是,指出是第几项,并求出该项以前所有项的和(不含265),若不是,说明理由.
}中的项,若是,指出是第几项,并求出该项以前所有项的和(不含265),若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设数列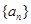 ,
,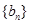 ,
,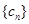 ,已知
,已知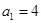 ,
,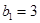 ,
,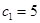 ,
,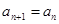 ,
,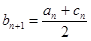 ,
,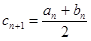 (
(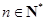 ).
).
(1)求数列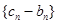 的通项公式;
的通项公式;
(2)求证:对任意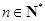 ,
, 为定值;
为定值;
(3)设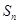 为数列
为数列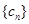 的前
的前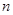 项和,若对任意
项和,若对任意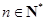 ,都有
,都有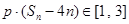 ,求实数
,求实数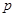 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com