
【题目】已知函数![]() .
.
(1)若![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的取值范围,并证明:对任意的
的取值范围,并证明:对任意的![]() ,都有
,都有![]()
(2)设![]() .讨论方程
.讨论方程![]() 实数根的个数
实数根的个数
【答案】(1)![]() ;证明见解析(2)当
;证明见解析(2)当![]() 时,方程
时,方程![]() 有一个实数解;当
有一个实数解;当![]() 时,方程
时,方程![]() 有两个不同的实数解;当
有两个不同的实数解;当![]() 时,方程
时,方程![]() 没有实数解
没有实数解
【解析】
(1)![]() 在
在![]() 上恒成立,分离参数得
上恒成立,分离参数得![]() ,只需
,只需![]() ,设
,设![]() ,利用求导求出其最大值为
,利用求导求出其最大值为![]() ,因此
,因此![]() ;根据所证明不等式的结构特征,取
;根据所证明不等式的结构特征,取![]() ,
,![]() 在
在![]() 上成立,令
上成立,令![]() ,
,![]() ,即可证明不等式;
,即可证明不等式;
(2)由![]() ,分离参数可得
,分离参数可得![]() ,设
,设![]() ,通过求导求出
,通过求导求出![]() 单调区间,极值最值,以及函数值变化趋势,即可求出结论.
单调区间,极值最值,以及函数值变化趋势,即可求出结论.
(1)由![]() 可得,
可得,![]()
令![]() ,则
,则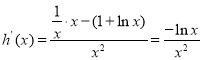
当![]() 时,
时,![]() 单调递增,
单调递增,
当![]() 时,
时,![]() 单调递减,
单调递减,
故![]() 在
在![]() 处取得极大值,也是最大值,
处取得极大值,也是最大值,
要使![]() ,只需
,只需![]() ,
,
故![]() 的取值范围为
的取值范围为![]() ,
,
显然,当![]() 时,有
时,有![]() ,
,
即不等式![]() 在
在![]() 上成立,
上成立,
令![]() ,则有
,则有![]()
所以![]() ,
,
即:![]() ;
;
(2)由![]() 可得,
可得,![]() ,
,
即![]() ,令
,令![]() ,
,
则![]() ,
,
当![]() 时,
时,![]() 单调递增,
单调递增,
当![]() 时,
时,![]() 单调递减,
单调递减,
故![]() 在
在![]() 处取得极大值
处取得极大值![]() ,也是最大值,
,也是最大值,
又当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
所以,当![]() 时,方程
时,方程![]() 有一个实数解;
有一个实数解;
当![]() 时,方程
时,方程![]() 有两个不同的实数解;
有两个不同的实数解;
当![]() 时,方程
时,方程![]() 没有实数解.
没有实数解.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】空气质量指数AQI是反映空气质量状况的指数,AQI指数值越小,表明空气质量越好,其对应关系如表:
AQI指数值 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 |
|
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
如图是某市12月1日-20日AQI指数变化趋势:

下列叙述正确的是( )
A.这20天中AQI指数值的中位数略高于100
B.这20天中的中度污染及以上的天数占![]()
C.该市12月的前半个月的空气质量越来越好
D.总体来说,该市12月上旬的空气质量比中旬的空气质量好
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型单位举行了一次全体员工都参加的考试,从中随机抽取了20人的分数.以下茎叶图记录了他们的考试分数(以十位数字为茎,个位数字为叶):

若分数不低于95分,则称该员工的成绩为“优秀”.
(1)从这20人中任取3人,求恰有1人成绩“优秀”的概率;
(2)根据这20人的分数补全下方的频率分布表和频率分布直方图,并根据频率分布直方图解决下面的问题.
组别 | 分组 | 频数 | 频率 |
|
1 |
| |||
2 |
| |||
3 |
| |||
4 |
|
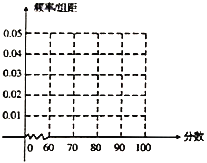
①估计所有员工的平均分数(同一组中的数据用该组区间的中点值作代表);
②若从所有员工中任选3人,记![]() 表示抽到的员工成绩为“优秀”的人数,求
表示抽到的员工成绩为“优秀”的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年春节前后,一场突如其来的新冠肺炎疫情在全国蔓延.疫情就是命令,防控就是责任.在党中央的坚强领导和统一指挥下,全国人民众志成城、团结一心,掀起了一场坚决打赢疫情防控阻击战的人民战争.下图表展示了2月14日至29日全国新冠肺炎疫情变化情况,根据该折线图,下列结论正确的是( )
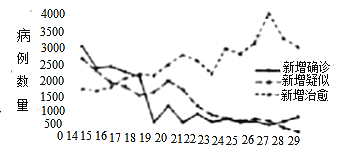
A.16天中每日新增确诊病例数量呈下降趋势且19日的降幅最大
B.16天中每日新增确诊病例的中位数小于新增疑似病例的中位数
C.16天中新增确诊、新增疑似、新增治愈病例的极差均大于2000
D.19日至29日每日新增治愈病例数量均大于新增确诊与新增疑似病例之和
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln (x+1)-![]() -x,a∈R.
-x,a∈R.
(1)当a>0时,求函数f(x)的单调区间;
(2)若存在x>0,使f(x)+x+1<-![]() (a∈Z)成立,求a的最小值.
(a∈Z)成立,求a的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关命题的说法正确的是( )
A.命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1”
B.“x=-1”是“x2-5x-6=0”的必要不充分条件
C.命题“若x=y,则sin x=sin y”的逆否命题为真命题
D.命题“x0∈R使得![]() ”的否定是“x∈R,均有x2+x+1<0”
”的否定是“x∈R,均有x2+x+1<0”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]() ,有以下三个结论:
,有以下三个结论:
①函数恒有两个零点,且两个零点之积为![]() ;
;
②函数的极值点不可能是![]() ;
;
③函数必有最小值.
其中正确结论的个数有( )
A.0个B.1个C.2个D.3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com