
【题目】已知函数f(x)=x2+2bx+c,且f(1)=f(3)=﹣1.设a>0,将函数f(x)的图像先向右平移a个单位长度,再向下平移a2个单位长度,得到函数g(x)的图像. (Ⅰ)若函数g(x)有两个零点x1 , x2 , 且x1<4<x2 , 求实数a的取值范围;
(Ⅱ)设连续函数在区间[m,n]上的值域为[λ,μ],若有 ![]() ,则称该函数为“陡峭函数”.若函数g(x)在区间[a,2a]上为“陡峭函数”,求实数a的取值范围.
,则称该函数为“陡峭函数”.若函数g(x)在区间[a,2a]上为“陡峭函数”,求实数a的取值范围.
【答案】解:(Ⅰ)由 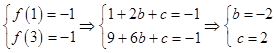 , 即f(x)=x2﹣4x+2,
, 即f(x)=x2﹣4x+2,
由题设可知g(x)=(x﹣a)2﹣4(x﹣a)+2﹣a2=x2﹣(2a+4)x+4a+2,
因为g(x)有两个零点x1 , x2 , 且x1<4<x2 ,
∴g(4)=16﹣4(2a+4)+4a+2<0, ![]() ,
,
又a>0,于是实数a的取值范围为 ![]() .
.
(Ⅱ)由g(x)=x2﹣(2a+4)x+4a+2可知,其对称轴为x=a+2,
①当0<a≤2时,a+2≥2a,函数g(x)在区间[a,2a]上单调递减,
最小值λ=g(2a)=﹣4a+2,最大值μ=g(a)=﹣a2+2,
则 ![]() ,显然此时a不存在,
,显然此时a不存在,
②当2<a≤4时,a<a+2<2a,最小值λ=g(a+2)=﹣a2﹣2,
又 ![]() ,最大值μ=g(a)=﹣a2+2,则
,最大值μ=g(a)=﹣a2+2,则 ![]() ,
, ![]() ,又2<a≤4,此时a亦不存在,
,又2<a≤4,此时a亦不存在,
③当a>4时,a<a+2<2a,最小值λ=g(a+2)=﹣a2﹣2,
又 ![]() ,故最大值μ=g(2a)=﹣4a+2,
,故最大值μ=g(2a)=﹣4a+2,
则 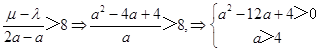 ,
, 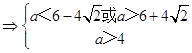 ,即
,即 ![]() ,
,
综上可知,实数a的取值范围为 ![]()
【解析】(Ⅰ)由f(1)=f(3)=﹣1求出b,c值,得到函数f(x)的解析式,进而可得函数g(x)的解析式,由函数g(x)有两个零点x1 , x2 , 且x1<4<x2 , 可得g(4)<0,解得实数a的取值范围; (Ⅱ)根据已知中“陡峭函数”的定义,结合二次函数的图像和性质,分类讨论,可得满足条件的实数a的取值范围.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos(ωx+ ![]() ),(ω>0,0<φ<π),其中x∈R且图象相邻两对称轴之间的距离为
),(ω>0,0<φ<π),其中x∈R且图象相邻两对称轴之间的距离为 ![]() ;
;
(1)求f(x)的对称轴方程和单调递增区间;
(2)求f(x)的最大值、最小值,并指出f(x)取得最大值、最小值时所对应的x的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P—ABCD中,平面PAD⊥底面ABCD,其中底面ABCD为等腰梯形,AD∥BC,PA=AB=BC=CD=2,PD=2![]() ,PA⊥PD,Q为PD的中点.
,PA⊥PD,Q为PD的中点.
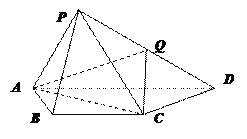
(Ⅰ)证明:CQ∥平面PAB;
(Ⅱ)求直线PD与平面AQC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义域为R的奇函数f(x)= ![]() ,其中h(x)是指数函数,且h(2)=4.
,其中h(x)是指数函数,且h(2)=4.
(1)求函数f(x)的解析式;
(2)求不等式f(2x﹣1)>f(x+1)的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过点P(m,n)的直线l与直线l0:x+2y+4=0垂直. (Ⅰ)若 ![]() ,且点P在函数
,且点P在函数 ![]() 的图像上,求直线l的一般式方程;
的图像上,求直线l的一般式方程;
(Ⅱ)若点P(m,n)在直线l0上,判断直线mx+(n﹣1)y+n+5=0是否经过定点?若是,求出该定点的坐标;否则,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某社区居民的家庭年收入与年支出的关系,相关部门随机调查了该社区5户家庭,得到如表统计数据表:
收入x(万元) | 8.2 | 8.6 | 10.0 | 11.3 | 11.9 |
支出y(万元) | 6.2 | 7.5 | 8.0 | 8.5 | 9.8 |
(1)根据上表可得回归直线方程 ![]() =
= ![]() x+
x+ ![]() ,其中
,其中 ![]() =0.76,
=0.76, ![]() =
= ![]() ﹣
﹣ ![]()
![]() ,据此估计,该社区一户年收入为15万元的家庭年支出为多少?
,据此估计,该社区一户年收入为15万元的家庭年支出为多少?
(2)若从这5个家庭中随机抽选2个家庭进行访谈,求抽到家庭的年收入恰好一个不超过10万元,另一个超过11万元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】张先生知道清晨从甲地到乙地有好、中、差三个班次的客车.但不知道具体谁先谁后.他打算:第一辆看后一定不坐,若第二辆比第一辆舒服,则乘第二辆;否则坐第三辆.问张先生坐到好车的概率和坐到差车的概率分别是( )
A.![]() 、
、 ![]()
B.![]() 、
、 ![]()
C.![]() 、
、 ![]()
D.![]() 、
、 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,g(x)=f(x)﹣a
,g(x)=f(x)﹣a
(1)当a=2时,求函数g(x)的零点;
(2)若函数g(x)有四个零点,求a的取值范围;
(3)在(2)的条件下,记g(x)得四个零点分别为x1 , x2 , x3 , x4 , 求x1+x2+x3+x4的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A、B、C所对的边分别是a、b、c,且a+b+c=8. (Ⅰ)若a=2,b= ![]() ,求cosC的值;
,求cosC的值;
(Ⅱ)若sinAcos2 ![]() +sinBcos2
+sinBcos2 ![]() =2sinC,且△ABC的面积S=
=2sinC,且△ABC的面积S= ![]() sinC,求a和b的值.
sinC,求a和b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com