
 ,若f(-4)=f(0),f(-2)=0,则关于x的不等式f(x)≤1的解集为( )
,若f(-4)=f(0),f(-2)=0,则关于x的不等式f(x)≤1的解集为( )| A.(-∞,-3]∪[-1,+∞) |
| B.[-3,-1] |
| C.[-3,-1]∪(0,+∞) |
| D.[-3,+∞) |
科目:高中数学 来源:不详 题型:解答题

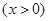 ,其中
,其中 ,
, 为正整数,
为正整数,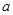 ,
, ,
, 均为常数,曲线
均为常数,曲线 在
在 处的切线方程为
处的切线方程为 .
.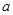 ,
, ,
, 的值;
的值;  的最大值;
的最大值; 都有
都有 .(
.( 为自然对数的底)
为自然对数的底)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 个单位的药剂后,经过x天该药剂在水中释放的浓度y(毫克/升)满足y=mf(x),其中
个单位的药剂后,经过x天该药剂在水中释放的浓度y(毫克/升)满足y=mf(x),其中 ,当药剂在水中释放的浓度不低于6(毫克/升)时称为有效净化;当药剂在水中释放的浓度不低于6(毫克/升)且不高于18(毫克/升)时称为最佳净化.
,当药剂在水中释放的浓度不低于6(毫克/升)时称为有效净化;当药剂在水中释放的浓度不低于6(毫克/升)且不高于18(毫克/升)时称为最佳净化.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
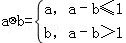 .设函数f(x)=(x2﹣2)?(x﹣x2),x∈R.若函数y=f(x)﹣c的图象与x轴恰有两个公共点,则实数c的取值范围是( )
.设函数f(x)=(x2﹣2)?(x﹣x2),x∈R.若函数y=f(x)﹣c的图象与x轴恰有两个公共点,则实数c的取值范围是( )A. |
B. |
C. |
D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com