
【题目】设函数![]() ,
, ![]() 为正实数.
为正实数.
(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)求证: ![]() ;
;
(3)若函数![]() 有且只有
有且只有![]() 个零点,求
个零点,求![]() 的值.
的值.
【答案】(1)![]() (2)详见解析(3)
(2)详见解析(3)![]() .
.
【解析】试题分析:(1)由导数几何意义得![]() ,所以先求导数
,所以先求导数![]() ,代入即得
,代入即得![]() ,又
,又![]() ,由点斜式得切线方程
,由点斜式得切线方程![]() (2)由于
(2)由于![]() ,所以转化为证明
,所以转化为证明![]() 恒成立,即
恒成立,即![]() ,转化为利用导数求函数最值
,转化为利用导数求函数最值![]() (3)因为
(3)因为![]() ,而
,而![]() 先增后减,且
先增后减,且![]() ,所以
,所以![]() 必为最大值(极大值),解得
必为最大值(极大值),解得![]() ,最后证明当1不为极值点时,
,最后证明当1不为极值点时, ![]() 的零点不唯一.
的零点不唯一.
试题解析:(1)当![]() 时,
时, ![]() ,则
,则![]() ,……………2分
,……………2分
所以![]() ,又
,又![]() ,
,
所以曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .…………4分
.…………4分
(2)因为![]() ,设函数
,设函数![]() ,
,
则![]() , …………………………………………………6分
, …………………………………………………6分
令![]() ,得
,得![]() ,列表如下:
,列表如下:
|
|
|
|
|
|
|
|
|
| 极大值 |
|
所以![]() 的极大值为
的极大值为![]() .
.
所以![]() .………………………………………………8分
.………………………………………………8分
(3)![]() ,
, ![]() ,
,
令![]() ,得
,得![]() ,因为
,因为![]() ,
,
所以![]() 在
在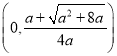 上单调增,在
上单调增,在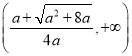 上单调减.
上单调减.
所以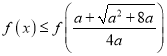 .………………………………………………10分
.………………………………………………10分
设![]() ,因为函数
,因为函数![]() 只有1个零点,而
只有1个零点,而![]() ,
,
所以![]() 是函数
是函数![]() 的唯一零点.
的唯一零点.
当![]() 时,
时, ![]() ,
, ![]() 有且只有
有且只有![]() 个零点,
个零点,
此时![]() ,解得
,解得![]() .…………………………………………12分
.…………………………………………12分
下证,当![]() 时,
时, ![]() 的零点不唯一.
的零点不唯一.
若![]() ,则
,则![]() ,此时
,此时![]() ,即
,即![]() ,则
,则![]() .
.
由(2)知, ![]() ,又函数
,又函数![]() 在以
在以![]() 和
和![]() 为端点的闭区间上的图象不间断,
为端点的闭区间上的图象不间断,
所以在![]() 和
和![]() 之间存在
之间存在![]() 的零点,则
的零点,则![]() 共有2个零点,不符合题意;
共有2个零点,不符合题意;
若![]() ,则
,则![]() ,此时
,此时![]() ,即
,即![]() ,则
,则![]() .
.
同理可得,在![]() 和
和![]() 之间存在
之间存在![]() 的零点,则
的零点,则![]() 共有2个零点,不符合题意.
共有2个零点,不符合题意.
因此![]() ,所以
,所以![]() 的值为
的值为![]() .…………………………………………………16分
.…………………………………………………16分


科目:高中数学 来源: 题型:
【题目】下列说法:
①频率是反映事件发生的频繁程度,概率反映事件发生的可能性大小;
②做n次随机试验,事件A发生m次,则事件A发生的频率![]() 就是事件A的概率;
就是事件A的概率;
③百分率是频率,但不是概率;
④频率是不能脱离n次试验的试验值,而概率是具有确定性的不依赖于试验次数的理论值;
⑤频率是概率的近似值,概率是频率的稳定值.
其中正确的是____(填序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个学生在一次竞赛中要回答![]() 道题是这样产生的:从
道题是这样产生的:从![]() 道物理题中随机抽取
道物理题中随机抽取![]() 道;从
道;从![]() 道化学题中随机抽取
道化学题中随机抽取![]() 道;从
道;从![]() 道生物题中随机抽取
道生物题中随机抽取![]() 道.使用合适的方法确定这个学生所要回答的三门学科的题的序号(物理题的编号为
道.使用合适的方法确定这个学生所要回答的三门学科的题的序号(物理题的编号为![]() ,化学题的编号为
,化学题的编号为![]() ,生物题的编号为
,生物题的编号为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图7.

(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差;
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
以直角坐标系的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立坐标系,已知点
轴的正半轴为极轴建立坐标系,已知点![]() 的直角坐标为
的直角坐标为![]() ,若直线
,若直线![]() 的极坐标方程为
的极坐标方程为![]() .曲线
.曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).
为参数).
(1)求直线![]() 和曲线
和曲线![]() 的普通方程;
的普通方程;
(2)设直线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某次考试中,语文成绩服从正态分布![]() ,数学成绩的频率分布直方图如下:
,数学成绩的频率分布直方图如下:

(Ⅰ)如果成绩大于135的为特别优秀,随机抽取的500名学生在本次考试中语文、数学成绩特别优秀的大约各多少人?(假设数学成绩在频率分布直方图中各段是均匀分布的)
(Ⅱ)如果语文和数学两科都特别优秀的共有6人,从(Ⅰ)中至少有一科成绩特别优秀的同学中随机抽取3人,设3人中两科都特别优秀的有![]() 人,求
人,求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)根据以上数据,是否有99%的把握认为语文特别优秀的同学,数学也特别优秀.
(附公及表)
①若![]() ,则
,则![]() ,
, ![]() ;
;
② ,
, ![]() ;
;
③

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com