分析:(I)由题意知
Q1(1,1),P1(1,),
Q2(,),P2(,),Q3(,),P3(,),Q4(,),由此可知
a1=,a2=,a3=.(II)由(I)可猜想
an=(n∈N*),然后用数学归纳法证明.
(III)由题意知x
n=(x
n-x
n-1)+(x
n-1-x
n-2)++(x
2-x
1)+x
1=
2-(n-1)+2-(n-2)++2-1+1==2-21-n,由此可知
an•bn=(xn+1-xn)•(yn-yn+1)=2-n(-)=(-)=
,所以
Sn=(a1b1+a2b2++anbn)≤(+++)=•=(1-)<. 解答:解:(I)由题意知
Q1(1,1),P1(1,),
Q2(,),P2(,),Q3(,),P3(,),Q4(,),
∴
a1=,a2=,a3=.(2分)
(II)由(I)猜想
an=(n∈N*),
下面用数学归纳法证明;
(1)当n=1时,
a1=已证得成立;
(2)假设当n=k时,猜想成立,
即
ak=,由已知得:
ak==xk+1-xk.当n=k+1时,由
ak+1=xk+2-xk+1=-∵
yk+2=,yk+1=,
∴a
k+1=(x
k+1+2
-k-1)-(x
k+2
-k)
=(x
k+1-x
k)+(2
-k-1-2
-k)
=2
-k+(2
-k-1-2
-k)
=
2-k-1=.所以当n=k+1时,猜想也成立,综合(1)(2)得
an=(n∈N*)(6分)
(III)x
n=(x
n-x
n-1)+(x
n-1-x
n-2)++(x
2-x
1)+x
1=
2-(n-1)+2-(n-2)++2-1+1==2-21-n(8分)
∴
an•bn=(xn+1-xn)•(yn-yn+1)=2-n(-)=(-)=
∵2•2
n-2≥2
n,2•2
n-1≥3,∴
an•bn≤,(10分)
∴
Sn=(a1b1+a2b2++anbn)≤(+++)=•=(1-)<.(12分)
点评:本题考查数列性质的综合应用,解题时要认真审题,仔细解答.

 如图,已知曲线C:y=
如图,已知曲线C:y=


 智能训练练测考系列答案
智能训练练测考系列答案 如图,已知曲线C:y=
如图,已知曲线C:y= (2006•南京二模)如图,已知曲线C:y=
(2006•南京二模)如图,已知曲线C:y=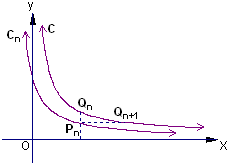 如图,已知曲线C:y=
如图,已知曲线C:y= 如图,已知曲线C:y=x2(0≤x≤1),O(0,0),Q(1,0),R(1,1).取线段OQ的中点A1,过A1作x轴的垂线交曲线C于P1,过P1作y轴的垂线交RQ于B1,记a1为矩形A1P1B1Q的面积.分别取线段OA1,P1B1的中点A2,A3,过A2,A3分别作x轴的垂线交曲线C于P2,P3,过P2,P3分别作y 轴的垂线交A1P1,RB1于B2,B3,记a2为两个矩形A2P2B2A1与矩形A3P3B3B1的面积之和.以此类推,记an为2n-1个矩形面积之和,从而得数列{an},设这个数列的前n项和为Sn.
如图,已知曲线C:y=x2(0≤x≤1),O(0,0),Q(1,0),R(1,1).取线段OQ的中点A1,过A1作x轴的垂线交曲线C于P1,过P1作y轴的垂线交RQ于B1,记a1为矩形A1P1B1Q的面积.分别取线段OA1,P1B1的中点A2,A3,过A2,A3分别作x轴的垂线交曲线C于P2,P3,过P2,P3分别作y 轴的垂线交A1P1,RB1于B2,B3,记a2为两个矩形A2P2B2A1与矩形A3P3B3B1的面积之和.以此类推,记an为2n-1个矩形面积之和,从而得数列{an},设这个数列的前n项和为Sn.