
分析 根据题意,由于函数f(x)是定义在R上的奇函数,则有f(0)=0,代入数据,计算可得a的值,对f(x)的表达式变形,用作差法判断函数单调性即可.
解答 解:∵函数$f(x)=\frac{{{2^x}-a}}{{{2^x}+a}}$为奇函数,实数a>0,
∴有f(0)=0,即$\frac{1-a}{1+a}$=0,解可得a=1,∴f(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$;
f(x)=1-$\frac{2}{{2}^{x}+1}$
理由:设x1<x2,
则f(x1)-f(x2)=$\frac{2({2}^{{x}_{1}}-{2}^{{x}_{2}})}{({2}^{{x}_{1}}+1)({2}^{{x}_{2}}+1)}$,
∵x1<x2,∴f(x1)-f(x2)<0,
∴f(x)是增函数.
点评 本题考查函数的单调性、奇偶性,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $m≤\frac{3}{2}\;,\;\;n=\frac{5}{2}$ | B. | m≤3,n=2 | C. | $m>\frac{3}{2}$ | D. | m>3,n=2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
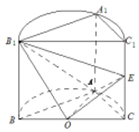 如图,已知平面BCC1B1是圆柱的轴截面(经过圆柱的轴截面)BC是圆柱底面的直径,O为底面圆心,E为母线CC1的中点,已知AB=AC=AA1=4
如图,已知平面BCC1B1是圆柱的轴截面(经过圆柱的轴截面)BC是圆柱底面的直径,O为底面圆心,E为母线CC1的中点,已知AB=AC=AA1=4查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com