
【题目】设函数![]() (
(![]() ),已知
),已知![]() 在
在![]() 有且仅有3个零点,下列结论正确的是( )
有且仅有3个零点,下列结论正确的是( )
A.在![]() 上存在
上存在![]() ,
,![]() ,满足
,满足![]()
B.![]() 在
在![]() 有且仅有1个最小值点
有且仅有1个最小值点
C.![]() 在
在![]() 单调递增
单调递增
D.![]() 的取值范围是
的取值范围是![]()
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源: 题型:
【题目】给出以下四个命题:
①数列![]() 为等差数列的充要条件是其通项公式为n的一次函数.
为等差数列的充要条件是其通项公式为n的一次函数.
②在面积为S的![]() 的边AB上任取一点P,则
的边AB上任取一点P,则![]() 的面积大于
的面积大于![]() 的概率为
的概率为![]() .
.
③将多项式![]() 分解因式得
分解因式得![]() ,则
,则![]() .
.
④若那么由![]() ,那么由
,那么由![]() 以及x轴所围成的图形一定在x轴下方.
以及x轴所围成的图形一定在x轴下方.
其中正确命题的序号为_____________(把所有正确命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高三数学考试中,一般有一道选做题,学生可以从选修4-4和选修4-5中任选一题作答,满分10分.某高三年级共有1000名学生参加了某次数学考试,为了了解学生的作答情况,计划从该年级1000名考生成绩中随机抽取一个容量为10的样本,为此将1000名考生的成绩按照随机顺序依次编号为000~999.
(1)若采用系统抽样法抽样,从编号为000~999的成绩中随机确定的编号为026,求样本中的最大编号.
(2)若采用分层抽样法,按照学生选择选修4-4或选修4-5的情况将成绩分为两层,已知该校共有600名考生选择了选修4-4,400名考生选择了选修4-5,在选取的样本中,选择选修4-4的平均得分为6分,方差为2,选择选修4-5的平均得分为5分,方差为0.75.用样本估计该校1000名考生选做题的平均得分和得分的方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC﹣A1B1C1中,∠ACB=90°,∠ABC=45°,AB=AA1=2,P为CC1的中点.
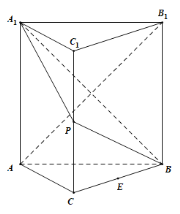
(1)证明:AB1⊥平面PA1B;
(2)设E为BC的中点,线段AB1上是否存在一点Q,使得QE∥平面A1ACC1?若存在,求四棱锥Q﹣AA1C1C的体积;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点M是圆C:(x+1)2+y2=8上的动点,定点D(1,0),点P在直线DM上,点N在直线CM上,且满足![]() 2
2![]() ,
,![]()
![]() 0,动点N的轨迹为曲线E.
0,动点N的轨迹为曲线E.
(1)求曲线E的方程;
(2)若AB是曲线E的长为2的动弦,O为坐标原点,求△AOB面积S的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,过
,过![]() 作直线
作直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 的周长为8.
的周长为8.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)问:![]() 的内切圆面积是否有最大值?若有,试求出最大值;若没有,说明理由.
的内切圆面积是否有最大值?若有,试求出最大值;若没有,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】足球运动是一项古老的体育活动,众多的资料表明,中国古代足球的出现比欧洲早,历史更为悠久,如图,现代比赛用足球是由正五边形与正六边形构成的共32个面的多面体,著名数学家欧拉证明了凸多面体的面数(F),顶点数(V),棱数(E)满足F+V-E=2,那么,足球有______.个正六边形的面,若正六边形的边长为![]() ,则足球的直径为______.cm(结果保留整数)(参考数据
,则足球的直径为______.cm(结果保留整数)(参考数据![]()

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+4[sin(θ+![]() )]x﹣2,θ∈[0,2π].
)]x﹣2,θ∈[0,2π].
(Ⅰ)若函数f(x)为偶函数,求tanθ的值;
(Ⅱ)若f(x)在[﹣![]() ,1]上是单调函数,求θ的取值范围.
,1]上是单调函数,求θ的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com