
BQ=BP且点S、A、B、Q及P、A、D、R共线,沿虚线将它们折叠成四棱锥,使P、Q、R、S四点重合为S.
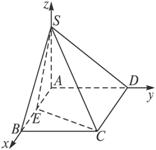
(1)请画出四棱锥S—ABCD的示意图,并证明SA⊥底面ABCD;
(2)若E为AB中点,求二面角ESCD的大小;
(3)求D到面SEC的距离.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com