
【题目】已知函数![]() .
.
⑴求函数![]() 的单调区间;
的单调区间;
⑵如果对于任意的![]() ,
,![]() 总成立,求实数
总成立,求实数![]() 的取值范围.
的取值范围.
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:高中数学 来源: 题型:
【题目】树林的边界是直线![]() (如图
(如图![]() 所在的直线),一只兔子在河边喝水时发现了一只狼,兔子和狼分别位于
所在的直线),一只兔子在河边喝水时发现了一只狼,兔子和狼分别位于![]() 的垂线
的垂线![]() 上的点
上的点![]() 点和
点和![]() 点处,
点处,![]() (
(![]() 为正常数),若兔子沿
为正常数),若兔子沿![]() 方向以速度
方向以速度![]() 向树林逃跑,同时狼沿线段
向树林逃跑,同时狼沿线段![]() 方向以速度
方向以速度![]() 进行追击(
进行追击(![]() 为正常数),若狼到达
为正常数),若狼到达![]() 处的时间不多于兔子到达M处的时间,狼就会吃掉兔子.
处的时间不多于兔子到达M处的时间,狼就会吃掉兔子.
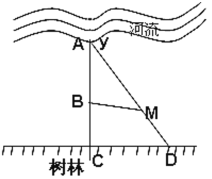
(1)求兔子的所有不幸点(即可能被狼吃掉的点)的区域面积![]() ;
;
(2)若兔子要想不被狼吃掉,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在“数学发展史”知识测验后,甲、乙、丙三人对成绩进行预测:
甲说:我的成绩比乙高;
乙说:丙的成绩比我和甲的都高;
丙说:我的成绩比乙高.
成绩公布后,三人成绩互不相同且只有一个人预测正确,那么三人中预测正确的是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,过点
,过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() 两点,延长
两点,延长![]() 交椭圆
交椭圆![]() 于点
于点![]() ,
,![]() 的周长为8.
的周长为8.
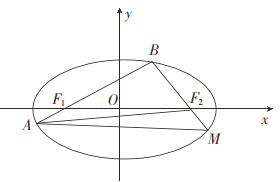
(1)求![]() 的离心率及方程;
的离心率及方程;
(2)试问:是否存在定点![]() ,使得
,使得![]() 为定值?若存在,求
为定值?若存在,求![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠APC=90°,∠BPD=120°,PB=PD.
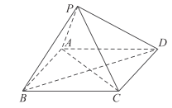
(1)求证:平面APC⊥平面BPD;
(2)若AB=2AP=2,求三棱锥C-PBD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,过点
,过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() 两点,
两点,![]() 的周长为8,直线
的周长为8,直线![]() 被椭圆
被椭圆![]() 截得的线段长为
截得的线段长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 是椭圆上两动点,线段
是椭圆上两动点,线段![]() 的中点为
的中点为![]() ,
,![]() 的斜率分别为
的斜率分别为![]() (
(![]() 为坐标原点),且
为坐标原点),且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,E,F分别为A1C1和BC的中点,M,N分别为A1B和A1C的中点.求证:
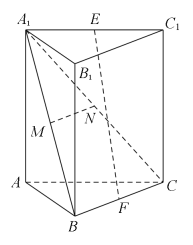
(1)MN∥平面ABC;
(2)EF∥平面AA1B1B.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com