
【题目】如图,在直三棱柱![]() 中,平面
中,平面![]() 侧面
侧面![]() ,且
,且![]() .
.
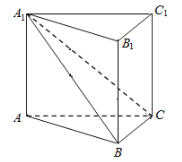
(1)求证:![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() ,求锐二面角
,求锐二面角![]() 的大小.
的大小.
【答案】见解析
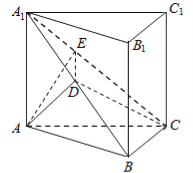
【解析】(1)如图,取![]() 的中点
的中点![]() ,连接
,连接![]() .
.
因为![]() ,所以
,所以![]() .
.
由平面![]() 侧面
侧面![]() ,且平面
,且平面![]() 侧面
侧面![]() ,
,
得![]() 平面
平面![]() . ………………(3分)
. ………………(3分)
又![]() 平面
平面![]() ,所以
,所以![]() ,
,
因为三棱柱![]() 是直三棱柱,则
是直三棱柱,则![]() 底面
底面![]() ,
,
所以![]()
又![]() ,从而
,从而![]() 侧面
侧面![]() ,又
,又![]() 侧面
侧面![]() ,
,
故![]() . ………………(6分)
. ………………(6分)
(2)解法一:连接![]() ,由(1)可知
,由(1)可知![]() 平面
平面![]() ,则
,则![]() 是
是![]() 在平面
在平面![]() 内的射影.
内的射影.
∴![]() 即为直线
即为直线![]() 与平面
与平面![]() 所成的角,则
所成的角,则![]() .
.
在等腰直角![]() 中,
中,![]() ,且点
,且点![]() 是
是![]() 中点,
中点,
∴![]() ,又
,又![]() ,
,![]() ,∴
,∴![]() .
.
过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,由(1)知
,由(1)知![]() 平面
平面![]() ,则
,则![]() ,又
,又![]() ,∴
,∴![]() ,
,
∴![]() 即为二面角
即为二面角![]() 的一个平面角. ………………(9分)
的一个平面角. ………………(9分)
在直角![]() 中,
中,![]() ,
,
又![]() ,
,![]() ,
,
∴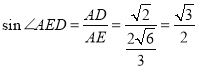 ,
,
又二面角![]() 为锐二面角,∴
为锐二面角,∴![]() ,
,
即二面角![]() 的大小为
的大小为![]() . ………………(12分)
. ………………(12分)
解法二(向量法):由(1)知![]() 且
且![]() 底面
底面![]() ,所以以点
,所以以点![]() 为原点,以
为原点,以![]() 所在直线分别为
所在直线分别为![]() ,
,![]() ,
,![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() .
.
设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
设平面![]() 的一个法向量
的一个法向量![]() ,由
,由![]() ,
,![]() ,得
,得![]() .
.
令![]() ,得
,得![]() ,则
,则![]() .
.
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,则
,则![]() ,
,
所以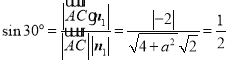 ,
,
解得![]() , 即
, 即![]() .
.
又设平面![]() 的一个法向量为
的一个法向量为![]() ,同理可得
,同理可得![]() .
.
设锐二面角![]() 的大小为
的大小为![]() ,则
,则![]() ,
,
由![]() ,得
,得![]() .
.
∴锐二面角![]() 的大小为
的大小为![]() . ………………(12分)
. ………………(12分)
【命题意图】本小题主要考查线线垂直,线面垂直,二面角等基础知识,考查推理论证能力、运算求解能力、空间想象能力,并考查应用向量知识解决立体几何问题的能力.


科目:高中数学 来源: 题型:
【题目】数列{an}中,a1=![]() ,前n项和Sn满足Sn+1-Sn=(
,前n项和Sn满足Sn+1-Sn=(![]() )n+1(n∈N*).
)n+1(n∈N*).
(1)求数列{an}的通项公式an以及前n项和Sn;
(2)若S1,t(S1+S2),3(S2+S3)成等差数列,求实数t的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}满足a1=1,nan+1=(n+1)an+n(n+1),n∈N* . (Ⅰ)证明:数列{ ![]() }是等差数列;
}是等差数列;
(Ⅱ)设bn=3n ![]() ,求数列{bn}的前n项和Sn .
,求数列{bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先后随机投掷2枚正方体骰子,其中x表示第1枚骰子出现的点数,y表示第2枚骰子出现的点数,
(1)求点P(x,y)在直线y=x﹣1上的概率;
(2)求点P(x,y)满足y2<4x的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一举行了一次数学竞赛,为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为n)进行统计,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在[50,60),[90,100]的数据). 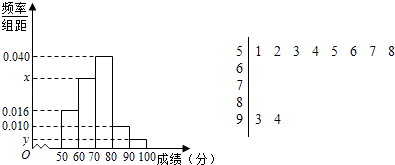
(1)求样本容量n和频率分布直方图中的x,y的值;
(2)估计本次竞赛学生成绩的中位数和平均分;
(3)在选取的样本中,从竞赛成绩在80分以上(含80分)的学生中随机抽取2名学生,求所抽取的2名学生中至少有一人得分在[90,100]内的频率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() . 问:是否存在正数m,使得对于任意正数
. 问:是否存在正数m,使得对于任意正数![]() ,可使
,可使![]() 为三角形的三边构成三角形?如果存在:①试写出一组x,y,m的值,②求出所有m的值;如果不存在,请说明理由.
为三角形的三边构成三角形?如果存在:①试写出一组x,y,m的值,②求出所有m的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,以原点O为圆心,椭圆C的长半轴长为半径的圆与直线
,以原点O为圆心,椭圆C的长半轴长为半径的圆与直线![]() 相切.
相切.
⑴求椭圆C的标准方程;
⑵已知点A、B为动直线![]() 与椭圆C的两个交点,问:在x轴上是否存在定点E,使得
与椭圆C的两个交点,问:在x轴上是否存在定点E,使得![]() 为定值?若存在,试求出点E的坐标和定值;若不存在,请说明理由.
为定值?若存在,试求出点E的坐标和定值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设常数a∈R,函数f(x)=(a﹣x)|x|.
(1)若a=1,求f(x)的单调区间;
(2)若f(x)是奇函数,且关于x的不等式mx2+m>f[f(x)]对所有的x∈[﹣2,2]恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,tanA是以﹣4为第三项,4为第七项的等差数列的公差,tanB是以2为公差,9为第五项的等差数列的第二项,则这个三角形是( )
A.锐角三角形
B.钝角三角形
C.等腰直角三角形
D.等腰或直角三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com