
【题目】已知函数![]() 恰有两个极值点
恰有两个极值点![]() .
.
(1)求实数![]() 的取值范围;
的取值范围;
(2)求证: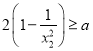 ;
;
(3)求证: ![]() (其中
(其中![]() 为自然对数的底数).
为自然对数的底数).
科目:高中数学 来源: 题型:
【题目】[选修4―4:坐标系与参数方程]
在直角坐标系xOy中,曲线C的参数方程为![]() (θ为参数),直线l的参数方程为
(θ为参数),直线l的参数方程为![]() .
.
(1)若a=1,求C与l的交点坐标;
(2)若C上的点到l的距离的最大值为![]() ,求a.
,求a.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面五边形ABCDE中,AB∥CE,且AE=2,∠AEC=60°,CD=ED=![]() ,cos∠EDC=
,cos∠EDC=![]() .将△CDE沿CE折起,使点D移动到P的位置,且AP=
.将△CDE沿CE折起,使点D移动到P的位置,且AP=![]() ,得到四棱锥P-ABCE.
,得到四棱锥P-ABCE.
(1)求证:AP⊥平面ABCE;
(2)记平面PAB与平面PCE相交于直线l,求证:AB∥l.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】本着健康、低碳的生活理念,租用公共自行车骑行的人越来越多.某种公共自行车的租用收费标准为:每次租车不超过1小时免费,超过1小时的部分每小时收费2元(不足1小时的部分按1小时计算).甲、乙两人相互独立来租车,每人各租1辆且租用1次.设甲、乙不超过1小时还车的概率分别为![]() 和
和![]() ;1小时以上且不超过2小时还车的概率分别为
;1小时以上且不超过2小时还车的概率分别为![]() 和
和![]() ;两人租车时间都不会超过3小时.
;两人租车时间都不会超过3小时.
(1) 求甲、乙两人所付租车费用相同的概率;
(2) 记甲、乙两人所付的租车费用之和为随机变量![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有一款智能学习APP,学习内容包含文章学习和视频学习两类,且这两类学习互不影响.已知该APP积分规则如下:每阅读一篇文章积1分,每日上限积5分;观看视频累计3分钟积2分,每日上限积6分.经过抽样统计发现,文章学习积分的概率分布表如表1所示,视频学习积分的概率分布表如表2所示.

(1)现随机抽取1人了解学习情况,求其每日学习积分不低于9分的概率;
(2)现随机抽取3人了解学习情况,设积分不低于9分的人数为![]() ,求
,求![]() 的概率分布及数学期望.
的概率分布及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:x+y-6=0,过直线上一点P作圆x2+y2=4的切线,切点分别为A,B,则四边形PAOB面积的最小值为______,此时四边形PAOB外接圆的方程为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《厉害了,我的国》是2018年在我国各影院上映的一部非常火的电影纪录片,该部影片主要讲述了我国近几年的发展现状和成就,影片通过讲述中国故事,刻画中国面貌,弘扬了中国精神,引起了国民的高度关注,上映仅半个月影片票房就突破了3亿元,刷新了我国纪录片的票房纪录,某市一电影院为了解该影院观看《厉害了,我的国》的观众的年龄构成情况,随机抽取了40名观众数据统计如表:
年龄/岁 | [10,20) | [20,30) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80) |
人数 | 6 | 8 | 12 | 6 | 4 | 2 | 2 |
(1)求所调查的40名观众年龄的平均数和中位数;
(2)该电影院决定采用抽奖方式来提升观影人数,将《厉害了,我的国》的电影票票价提高20元/张,并允许购买电影票的观众抽奖3次,中奖1次、2次、3次分别奖现金20元、30元、60元,设观众每次中奖的概率均为![]() ,则观众在3次抽奖中所获得的奖金总额的数学期望是多少元(结果保留整数)?
,则观众在3次抽奖中所获得的奖金总额的数学期望是多少元(结果保留整数)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com