
【题目】已知函数![]() ,
,![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若存在与函数![]() ,
,![]() 的图象都相切的直线,求实数
的图象都相切的直线,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]()
【解析】
(1)对h(x)求导,得![]() ,对
,对![]() ,
,![]() 分别讨论,得单调区间;
分别讨论,得单调区间;
(2)设f(x)在点(x1,f(x1))与g(x)在点(x2,f(x2))处切线相同,则![]() ,分别求得导数和切线的斜率,构造新函数
,分别求得导数和切线的斜率,构造新函数![]()
![]() ,求出导数和单调区间,最值,运用单调性计算可得a的范围.
,求出导数和单调区间,最值,运用单调性计算可得a的范围.
(1)函数![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
所以![]()
所以当![]() 即
即![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 即
即![]() 时,
时,
当![]() 时
时![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,令
时,令![]() 得
得![]()
| | | |
| + | - | + |
| 增 | 减 | 增 |
综上:当![]() 时,
时,![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时
时![]() 在
在![]() ,
,![]() 单调递增,在
单调递增,在![]() 单调递减.
单调递减.
(2)设函数![]() 在点
在点![]() 与函数
与函数![]() 在点
在点![]() 处切线相同,
处切线相同,
![]() ,则
,则![]() ,
,
由![]() ,得
,得![]() ,再由
,再由![]()
得![]() ,把
,把![]() 代入上式得
代入上式得![]()
设![]() (∵x2>0,∴x∈(0,+∞)),
(∵x2>0,∴x∈(0,+∞)),
则![]() 不妨设
不妨设![]() .
.
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
所以![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
把![]() 代入可得:
代入可得:![]()
设![]() ,则
,则![]() 对
对![]() 恒成立,
恒成立,
所以![]() 在区间
在区间![]() 上单调递增,又
上单调递增,又![]()
所以当![]() 时
时![]() ,即当
,即当![]() 时
时![]() ,
,
又当![]() 时,
时,![]()
![]()
因此当![]() 时,函数
时,函数![]() 必有零点;即当
必有零点;即当![]() 时,必存在
时,必存在![]() 使得
使得![]() 成立;
成立;
即存在![]() 使得函数
使得函数![]() 在点
在点![]() 与函数
与函数![]() 在点
在点![]() 处切线相同.
处切线相同.
又由![]() 单调递增得,因此
单调递增得,因此![]()
所以实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】为了解甲、乙两厂的产品质量,采用分层抽样的方法从甲、乙两厂生产的产品中分别抽取14件和5件,测量产品中的微量元素x,y的含量(单位:毫克).下表是乙厂的5件产品的测量数据:
编号 | 1 | 2 | 3 | 4 | 5 |
x | 169 | 178 | 166 | 175 | 180 |
y | 75 | 80 | 77 | 70 | 81 |
已知甲厂生产的产品共有98件.
(1)求乙厂生产的产品数量;
(2)当产品中的微量元素x,y满足x≥175,且y≥75时,该产品为优等品,用上述样本数据估计乙厂生产的优等品的数量;
(3)从乙厂抽出的上述5件产品中,随机抽取2件,求抽取的2件产品中优等品数![]() 的分布列及其均值(即数学期望).
的分布列及其均值(即数学期望).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆W:![]() (a>b>0)的离心率
(a>b>0)的离心率![]() ,其右顶点A(2,0),直线l过点B(1,0)且与椭圆交于C,D两点.
,其右顶点A(2,0),直线l过点B(1,0)且与椭圆交于C,D两点.
(Ⅰ)求椭圆W的标准方程;
(Ⅱ)判断点A与以CD为直径的圆的位置关系,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】改革开放以来,中国经济飞速发展,科学技术突飞猛进。高铁、核电、桥梁、激光、![]() 通信、人工智能、航空航天、移动支付、量子通讯、特高压输电等许多技术都领先于世界。厉害了,我的国!把“厉害了我的国”这六个字随机地排成一排,其中“厉”、“害”这两个字必须相邻(可以交换顺序),“了”、“的”这两个助词不能相邻,则不同排法的种数为( )。
通信、人工智能、航空航天、移动支付、量子通讯、特高压输电等许多技术都领先于世界。厉害了,我的国!把“厉害了我的国”这六个字随机地排成一排,其中“厉”、“害”这两个字必须相邻(可以交换顺序),“了”、“的”这两个助词不能相邻,则不同排法的种数为( )。
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某食品厂制作了3种与“福”字有关的精美卡片,分别是“富强福”、“和谐福”、“友善福”,每袋食品随机装入一张卡片,若只有集齐3种卡片才可获奖,则购买该食品4袋,获奖的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方形![]() 的对角线
的对角线![]() 与
与![]() 相交于
相交于![]() 点,将
点,将![]() 沿对角线
沿对角线![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() (如图),则下列命题中正确的为
(如图),则下列命题中正确的为![]()
![]()

A.直线![]() 直线
直线![]() ,且直线
,且直线![]() 直线
直线![]()
B.直线![]() 平面
平面![]() ,且直线
,且直线![]() 平面
平面![]()
C.平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]()
D.平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某海域的东西方向上分别有A,B两个观测点(如图),它们相距![]() 海里.现有一艘轮船在D点发出求救信号,经探测得知D点位于A点北偏东45°,B点北偏西60°,这时,位于B点南偏西60°且与B点相距
海里.现有一艘轮船在D点发出求救信号,经探测得知D点位于A点北偏东45°,B点北偏西60°,这时,位于B点南偏西60°且与B点相距![]() 海里的C点有一救援船,其航行速度为30海里/小时.
海里的C点有一救援船,其航行速度为30海里/小时.

(1)求B点到D点的距离BD;
(2)若命令C处的救援船立即前往D点营救,求该救援船到达D点需要的时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
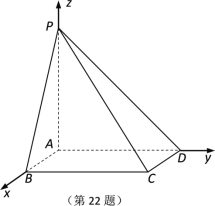
【题目】如图所示,在四棱锥![]() 中,底面
中,底面![]() 是矩形,
是矩形,![]() 平面
平面![]() ,AB 1,AP AD 2.
,AB 1,AP AD 2.
(1)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(2)若点M,N分别在AB,PC上,且![]() 平面
平面![]() ,试确定点M,N的位置.
,试确定点M,N的位置.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com