练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．三棱锥P-ABC中，面PBC和面ABC都是边长为12的正三角形，平面PBC和平面ABC所成二面角是60°，求点P到平面ABC的距离．

    分析 取BC的中点D，连接AD、PD．则PD垂直BC、AD垂直BC，∠PDA为二面角的平面角，作PE⊥AD于E．因为BC⊥平面ADP，所以BC⊥PE，故PE⊥平面ABC，从而PE即为所求距离．

    解答 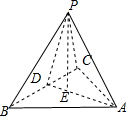解：取BC的中点D，连接AD、PD．则PD垂直BC、AD垂直BC，
    ∴∠PDA为二面角的平面角，故∠PDA=60°．
    作PE⊥AD于E．因为BC⊥平面ADP，所以BC⊥PE，故PE⊥平面ABC，
    从而PE即为所求距离．
    求得：PD=6$\sqrt{3}$，所以PE=PD$•\frac{\sqrt{3}}{2}$=9．

    点评 本题考查点面距离的计算，考查二面角，考查学生分析解决问题的能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    17．已知0≤x≤2求函数$y={（{\frac{1}{4}}）^{x-1}}-4{（{\frac{1}{2}}）^x}+2$的最大值与最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知P在抛物线y2=4x上，那么点P到点Q（2，1）的距离与点P到抛物线焦点距离之和取得最小值为（　　）
    A．2B．3C．4D．6

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．如图为从空中某个角度俯视北京奥运会主体育场“鸟巢”顶棚所得的局部示意图，在平面直角坐标系中，下列给定的一系列直线中（其中θ为参数，θ∈R），能形成这种效果的只可能是（　　）
    A．y=xsinθ+1B．y=x+cosθC．xcosθ+ysinθ+1=0D．y=xcosθ+sinθ

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知正项数列{an}中前n项和为Sn=$\frac{1}{2}$（an+$\frac{1}{{a}_{n}}$），求Sn及an．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．函数f（x）=-tan（$\frac{π}{3}$-2x）的单调递增区间是（　　）
    A．[$\frac{kπ}{2}$-$\frac{π}{12}$，$\frac{kπ}{2}$+$\frac{5π}{12}$]（k∈Z）B．（$\frac{kπ}{2}$-$\frac{π}{12}$，$\frac{kπ}{2}$+$\frac{5π}{12}$）（k∈Z）
    C．（kπ+$\frac{π}{6}$，kπ+$\frac{2π}{3}$）（k∈Z）D．[kπ-$\frac{π}{12}$，kπ+$\frac{5π}{12}$]（k∈Z）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知函数f（x）=$\frac{{e}^{x}}{{x}^{2}-mx+1}$
    （1）若m∈（-2，2），求函数y=f（x）的单调区间；
    （2）若m∈（0，$\frac{1}{2}$]，则当x∈[0，m+1]时，函数y=f（x）的图象是否总在直线y=x上方，请写出判断过程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知四棱锥P-ABCD，底面ABCD为正方形，侧面PAD为直角三角形，且PA=PD，面PAD⊥面ABCD，E、F分别为AB、PD的中点．
    （Ⅰ）求证：EF∥面PBC；
    （Ⅱ）求证：AP⊥面PCD．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．已知$sin（α+\frac{π}{2}）=\frac{3}{5}$，$α∈（-\frac{π}{2}，0）$，则tanα的值为$-\frac{4}{3}$．

    查看答案和解析>>

    同步练习册答案