
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,经过点
,经过点![]() 的直线与椭圆相交于
的直线与椭圆相交于![]() 两点,已知
两点,已知![]() 的周长为
的周长为![]() 。
。
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() ,求直线
,求直线![]() 的方程。
的方程。
科目:高中数学 来源: 题型:
【题目】已知复数z=![]() ,(m∈R,i是虚数单位).
,(m∈R,i是虚数单位).
(1)若z是纯虚数,求m的值;
(2)设![]() 是z的共轭复数,复数
是z的共轭复数,复数![]() +2z在复平面上对应的点在第一象限,求m的取值范围.
+2z在复平面上对应的点在第一象限,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】微信支付诞生于微信红包,早期知识作为社交的一部分“发红包”而诞生的,在发红包之余才发现,原来微信支付不仅可以用来发红包,还可以用来支付,现在微信支付被越来越多的人们所接受,现从某市市民中随机抽取300为对是否使用微信支付进行调查,得到下列![]() 的列联表:
的列联表:
年轻人 | 非年轻人 | 总计 | |
经常使用微信支付 | 165 | 225 | |
不常使用微信支付 | |||
合计 | 90 | 300 |
根据表中数据,我们得到的统计学的结论是:由__________的把握认为“使用微信支付与年龄有关”。
|
|
|
|
|
|
|
|
|
|
|
|
其中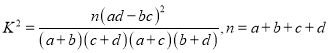
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)已知函数f(x)=![]()
(1)判断函数在区间[1,+∞)上的单调性,并用定义证明你的结论.
(2)求该函数在区间[1,4]上的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家庭进行理财投资,根据长期收益率市场预测,投资![]() 类产品的收益与投资额成正比,投资
类产品的收益与投资额成正比,投资![]() 类产品的收益与投资额的算术平方根成正比.已知投资1万元时
类产品的收益与投资额的算术平方根成正比.已知投资1万元时![]() 两类产品的收益分别为0.125万元和0.5万元.
两类产品的收益分别为0.125万元和0.5万元.
(1)分别写出![]() 两类产品的收益与投资额的函数关系;
两类产品的收益与投资额的函数关系;
(2)该家庭有20万元资金,全部用于理财投资,问:怎么分配资金能使投资获得最大收益,其最大收益是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 在定义域内为增函数,求实数
在定义域内为增函数,求实数![]() 的取值范围;
的取值范围;
(2)在(1)的条件下,若![]() ,
, ![]() ,
, ![]() ,求
,求![]() 的极小值;
的极小值;
(3)设![]() ,
, ![]() .若函数
.若函数![]() 存在两个零点
存在两个零点![]() ,且满足
,且满足![]() ,问:函数
,问:函数![]() 在
在![]() 处的切线能否平行于
处的切线能否平行于![]() 轴?若能,求出该切线方程,若不能,请说明理由.
轴?若能,求出该切线方程,若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次趣味校园运动会的颁奖仪式上,高一、高二、高三代表队人数分别为120人、120人、n人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就座,其中高二代表队有6人.

(1)求n的值;
(2)把在前排就座的高二代表队6人分别记为a,b,c,d,e,f,现随机从中抽取2人上台抽奖.求a和b至少有一人上台抽奖的概率;
(3)抽奖活动的规则是:代表通过操作按键使电脑自动产生两个[0,1]之间的均匀随机数x,y,并按如图所示的程序框图执行.若电脑显示“中奖”,则该代表中奖;若电脑显示“谢谢”,则不中奖,求该代表中奖的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com