
【题目】在平面直角坐标系xoy中,已知中心在原点,焦点在x轴上的双曲线C的离心率为![]() ,且双曲线C与斜率为2的直线l相交,且其中一个交点为P(﹣3,0).
,且双曲线C与斜率为2的直线l相交,且其中一个交点为P(﹣3,0).
(1)求双曲线C的方程及它的渐近线方程;
(2)求以直线l与坐标轴的交点为焦点的抛物线的标准方程.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)设出双曲线方程,利用点在双曲线以及双曲线的离心率求解即可.
(2)求出直线与坐标轴的交点,然后利用抛物线的性质求解抛物线方程即可.
试题解析:(1)由题意,设双曲线的方程为![]() ,∵点P(﹣3,0)在双曲线上,∴a=3.∵双曲线C的离心率为:
,∵点P(﹣3,0)在双曲线上,∴a=3.∵双曲线C的离心率为:![]() ,∴
,∴![]() ,∵c2=a2+b2,∴b=3,∴双曲线的方程为:
,∵c2=a2+b2,∴b=3,∴双曲线的方程为:![]() ,其渐近线方程为:y=±x.
,其渐近线方程为:y=±x.
(2)由题意,直线l的方程为y=2(x+3),即y=2x+6,直线l与坐标轴交点分别为F1(﹣3,0),F2(0,6),∴以F1(﹣2,0)为焦点的抛物线的标准方程为y2=﹣12x;以F2(0,4)为焦点的抛物线的标准方程为x2=24y.


科目:高中数学 来源: 题型:
【题目】某市积极倡导学生参与绿色环保活动,其中代号为“环保卫士—12369”的绿色环保活动小组对2014年1月—2014年12月(一年)内空气质量指数![]() 进行监测,下表是在这一年随机抽取的100天的统计结果:
进行监测,下表是在这一年随机抽取的100天的统计结果:
指数API | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] | >300 |
空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中重度污染 | 重度污染 |
天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
(1)若某市某企业每天由空气污染造成的经济损失![]() (单位:元)与空气质量指数
(单位:元)与空气质量指数![]() (记为
(记为![]() )的关系为:
)的关系为: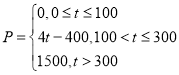 ,在这一年内随机抽取一天,估计该天经济损失
,在这一年内随机抽取一天,估计该天经济损失![]() 元的概率;
元的概率;
(2)若本次抽取的样本数据有30天是在供暖季节,其中有8天为重度污染,![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为某市本年度空气重度污染与供暖有关?
的把握认为某市本年度空气重度污染与供暖有关?
非重度污染 | 重度污染 | 合计 | |
供暖季 | |||
非供暖季节 | |||
合计 | 100 |
下面临界值表供参考.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的函数f(x)= ![]() 是奇函数,
是奇函数,
(1)求实数a的值;
(2)若对任意的t∈R,不等式f(t2﹣2t)+f(2t2﹣k)<0恒成立,求实数k的取值范围;
(3)设关于x的方程f(4x﹣b)+f(﹣2x+1)=0有实数根,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过
,过![]() 的左焦点
的左焦点![]() 的直线
的直线![]() ,直线
,直线![]() 被圆
被圆![]() :
:![]() 截得的弦长为
截得的弦长为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() 的右焦点为
的右焦点为![]() ,在圆
,在圆![]() 上是否存在点
上是否存在点![]() ,满足
,满足![]() ,若存在,指出有几个这样的点(不必求出点的坐标);若不存在,说明理由.
,若存在,指出有几个这样的点(不必求出点的坐标);若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
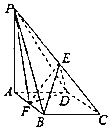
【题目】如图:在四棱锥P﹣ABCD中,底面ABCD是菱形,∠BAD=60°,AB=2,PA=3,PA⊥底面ABCD,E是PC中点,F是AB中点.
(Ⅰ)求证:BE∥平面PDF;
(Ⅱ)求直线PD与平面PFB所成角的正切值;
(Ⅲ)求三棱锥P﹣DEF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)已知抛物线![]() 的顶点在坐标原点
的顶点在坐标原点![]() ,对称轴为
,对称轴为![]() 轴,焦点为
轴,焦点为![]() ,抛物线上一点
,抛物线上一点![]() 的横坐标为
的横坐标为![]() ,且
,且![]() .
.
(Ⅰ)求此抛物线![]() 的方程;
的方程;
(Ⅱ)过点![]() 做直线
做直线![]() 交抛物线
交抛物线![]() 于
于![]() 两点,求证:
两点,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com