练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图所示,已知☉O1与☉O2相交于A,B两点,过点A作☉O1的切线交☉O2于点C,过点B作两圆的割线,分别交☉O1、☉O2于点D、E,DE与AC相交于点P.若AD是☉O2的切线,且PA=6,PC=2,BD=9,则AB的长为____.

    【答案】6

    【解析】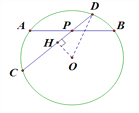

    试题分析：由 与 相切 ,再由切割线定理得

    ,再相交弦定理知 ,又由切割线定理可得 易证 , 所以 .

    试题解析：因为AC与☉O1相切,切点为A,所以∠BAC=∠ADB,

    又∠BAC=∠BEC,所以∠ADB=∠BEC.所以AD∥CE,所以△CPE∽△APD,

    所以,即CE=AD,因为AP为☉O1的切线,PBD为☉O1的割线,所以由切割线定理得PA2=PB·PD=PB·(PB+BD),即36=PB·(PB+9),解得,在☉O2中,由相交弦定理知PB·PE=PA·PC,即3PE=2×6,得PE=4,又因为AD为☉O2的切线,DBE为☉O2的割线,所以由切割线定理可得DA2=DB·DE,即DA2=9×(9+3+4),得DA=12,所以CE=4.

    易证△BPA∽△CPE,所以,所以AB=CE=6.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知 =（cosα，sinα）， =（cosβ，sinβ），0＜β＜α＜π．
    （1）若| ﹣ |= ，求证： ⊥ ；
    （2）设 =（0，1），若 + = ，求α，β的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{}中，，且对任意正整数都成立，数列{}的前n项和为Sn。

    （1）若，且，求a；

    （2）是否存在实数k，使数列{}是公比不为1的等比数列，且任意相邻三项按某顺序排列后成等差数列，若存在，求出所有k值，若不存在，请说明理由；

    （3）若。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

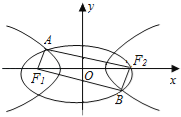
    【题目】如图F1、F2是椭圆C1：+y2=1与双曲线C2的公共焦点，A、B分别是C1、C2在第二、四象限的公共点，若四边形AF1BF2为矩形，则C2的离心率是（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知等比数列{an}满足：a1= ，a1 ， a2 ， a3﹣ 成等差数列，公比q∈（0，1）
    （1）求数列{an}的通项公式；
    （2）设bn=2nan ， 求数列{bn}的前n项和Sn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】用数学归纳法证明12+22+…+（n﹣1）2+n2+（n﹣1）2+…+22+12═ 时，由n=k的假设到证明n=k+1时，等式左边应添加的式子是（ ）
    A.（k+1）2+2k2
    B.（k+1）2+k2
    C.（k+1）2
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x2﹣2ax﹣2alnx（a∈R），则下列说法正确的是 ①当a＜0时，函数y=f（x）有零点；
    ②若函数y=f（x）有零点，则a＜0；
    ③存在a＞0，函数y=f（x）有唯一的零点；
    ④若函数y=f（x）有唯一的零点，则a≤1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司研究开发了一种新产品，生产这种新产品的年固定成本为150万元，每生产千件，需另投入成本为 (万元)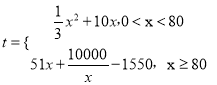， .每件产品售价为500元.该新产品在市场上供不应求可全部卖完.

    （Ⅰ）写出年利润（万元）关于年产量（千件）的函数解析式;

    （Ⅱ）当年产量为多少千件时，该公司在这一新产品的生产中所获利润最大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列各图中，不可能表示函数y=f（x）的图象的是（　　）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    同步练习册答案