
【题目】如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,PD=2,DC=BC=1,AB=2,AB∥DC,∠BCD=90°.
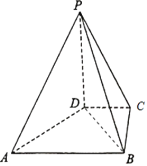
(1)求证:AD⊥PB;
(2)求A点到平面BPC的距离.
【答案】(1)证明见解析.(2)![]()
【解析】
(1)利用勾股定理证得AD⊥BD,又PD⊥平面ABCD,所以PD⊥AD,从而由线面垂直的判定定理得到AD⊥平面PBD,所以AD⊥PB;
(2)证得BC⊥PC,求出S△BPC和S△ABC,再由VA﹣BPC=VP﹣ABC 利用等体积法即可求出点A到平面PBC的距离.
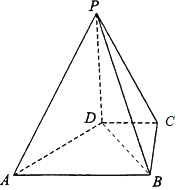
(1)如图所示:
在四边形ABCD中,连接BD,由DC=BC=1,AB=2,∠BCD=∠ABC![]() ,
,
在△ABD中,BD=AD![]() ,又AB=2,
,又AB=2,
因此AD⊥BD,又PD⊥平面ABCD,
∴PD⊥AD,又BD∩PD=D,
∴AD⊥平面PBD,
∴AD⊥PB;
(2)在四棱锥P﹣ABCD中,∵PD⊥平面ABCD,
∴PD⊥BC,而BC⊥DC,
∴BC⊥平面PDC,
∴BC⊥PC,又![]() ,
,
∴![]() ,而S△ABC
,而S△ABC![]() 1,
1,
,设点A到平面PBC的距离为h,
由VA﹣BPC=VP﹣ABC 可得:![]() ,
,
∴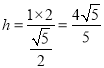 ,
,
即点A到平面PBC的距离为![]() .
.


科目:高中数学 来源: 题型:
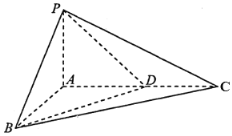
【题目】如图,已知三棱锥P-ABC中,PA平面ABC,ABAC,且PA=l,AB=AC=2,点D满足![]() ,
,![]() .
.
(1)当![]() ,求二面角P-BD-C的余弦值;
,求二面角P-BD-C的余弦值;
(2)若直线PC与平面PBD所成角的正弦值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次比赛中,某队的六名队员均获得奖牌,共获得4枚金牌2枚银牌,在颁奖晚会上,这六名队员与1名领队排成一排合影,若两名银牌获得者需站在领队的同侧,则不同的排法共有______种.(用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数),以原点
为参数),以原点![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴建立极坐标系,曲线
轴非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设点![]() ,
,![]() 分别是曲线
分别是曲线![]() ,
,![]() 上两动点且
上两动点且![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天上有些恒星的亮度是会变化的,其中一种称为造父(型)变星,本身体积会膨胀收缩造成亮度周期性的变化.第一颗被描述的经典造父变星是在1784年.
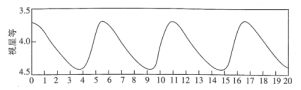
上图为一造父变星的亮度随时间的周期变化图,其中视星等的数值越小,亮度越高,则此变星亮度变化的周期、最亮时视星等,分别约是( )
A.5.5,3.7B.5.4,4.4C.6.5,3.7D.5.5,4.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com