
����Ŀ��![]() ������Ҷ���й���ѧ�Ҽ��ܸ�����ֱ�������ݵĶ���ʽϵ��������ͼ��ʾ�ǡ�����������㷨������������ԭ�����е�
������Ҷ���й���ѧ�Ҽ��ܸ�����ֱ�������ݵĶ���ʽϵ��������ͼ��ʾ�ǡ�����������㷨������������ԭ�����е�![]() �㼴Ϊ
�㼴Ϊ![]() չ��ʽ��ϵ�������ܳ���������Ϊ������������ԭ�������������������������δ��������ʽϵ����һ�㹫ʽ�����δ�ܽ���һ�����������ݵĶ���ʽ���������ܵ���ѧ������ʧ����
չ��ʽ��ϵ�������ܳ���������Ϊ������������ԭ�������������������������δ��������ʽϵ����һ�㹫ʽ�����δ�ܽ���һ�����������ݵĶ���ʽ���������ܵ���ѧ������ʧ����![]() ������ѧ������ڡ��������㷨��
������ѧ������ڡ��������㷨��![]() �������˿���������ԭͼ��ע����ͼ�����������������������ô������������������ֻ�Ǻ���������˰������Ϊ�������������
�������˿���������ԭͼ��ע����ͼ�����������������������ô������������������ֻ�Ǻ���������˰������Ϊ�������������![]() չ��ʽ��
չ��ʽ��![]() ��ϵ��Ϊ
��ϵ��Ϊ![]() ������ʵ��
������ʵ��![]() ��ֵΪ_______________����չ��ʽ�и���ϵ��֮��Ϊ__________________��
��ֵΪ_______________����չ��ʽ�и���ϵ��֮��Ϊ__________________��


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʮ�˴�ָ����������ǿ����������������г���������ɡ�ƽ�ȡ����������Σ�������������ҵ�����š�����.���ڴ�������������������������������������������������������ҵ����6����������ѡ2��������������һ�������Ǵӹ��Ҳ�������������ļ�ֵ�ۻ���������������ĸ�����________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ס�ڳ����![]() ��,����������λ
��,����������λ![]() ���ϰ�,���õظ�·�η����³��¼������������,����ͬһ·�η����³��¼����ֻ��һ��,�����³��¼��ĸ�����ͼ(���磺
���ϰ�,���õظ�·�η����³��¼������������,����ͬһ·�η����³��¼����ֻ��һ��,�����³��¼��ĸ�����ͼ(���磺![]() ��������·�Σ�·��
��������·�Σ�·��![]() �����³��¼��ĸ���Ϊ
�����³��¼��ĸ���Ϊ![]() ,·��
,·��![]() �����³��¼��ĸ���Ϊ
�����³��¼��ĸ���Ϊ![]() ).
).

(1)����Ϊ��ѡ��һ����![]() ��
��![]() �����·��
�����·��
(������ֻѡ������ʹ�����·��),
ʹ��;�з����³��¼��ĸ�����С��
(2)�����·��![]() �������Ķ³�����Ϊ�������
�������Ķ³�����Ϊ�������![]() ,��
,��![]() ����ѧ����
����ѧ����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ʒ��Ϊ���˽�ͻ����������µ������ͺ���������������������ȡ��һЩ�ͻ����лطã����������±���
�����ͺ� | I | II | III | IV | V |
�طÿͻ��������� | 250 | 100 | 200 | 700 | 350 |
������ | 0.5 | 0.3 | 0.6 | 0.3 | 0.2 |
��������ָ��ij���ͺ������Ļطÿͻ��У������������������ı�ֵ.
����ͻ��Ƿ����⻥���������ÿ���ͺ������ͻ����ڴ��ͺ���������ĸ���������и��ͺ����������������.
(1)�����еĻطÿͻ��������ȡ1�ˣ�������ͻ�����ĸ��ʣ�
(2)��I�ͺź�V�ͺ����������пͻ��и������ȡ1�ˣ����������������Ϊ![]() ����
����![]() �ķֲ��к�������
�ķֲ��к�������
(3)�� ��![]() ��, ��
��, ��![]() ��, ��
��, ��![]() ��, ��
��, ��![]() ��, ��
��, ��![]() ���ֱ��ʾI, II, III, IV, V�ͺ������ÿͻ����⣬ ��
���ֱ��ʾI, II, III, IV, V�ͺ������ÿͻ����⣬ ��![]() ��, ��
��, ��![]() ��, ��
��, ��![]() ��, ��
��, ��![]() ��, ��
��, ��![]() �� �ֱ��ʾI, II, III, IV, V�ͺ������ÿͻ�������.д������
�� �ֱ��ʾI, II, III, IV, V�ͺ������ÿͻ�������.д������![]() �Ĵ�С��ϵ.
�Ĵ�С��ϵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���й���ŷ��ij����ѧԺΪ���ø�������˽��й���ͳ�Ļ����ڵ��ؾٰ���һ���ɵ����˲μӵ��й���ͳ�Ļ�֪ʶ������Ϊ���˽�μӱ��δ���������Ա�ijɼ�������Ӳ�������Ա�������ȡ![]() ����Ա�ijɼ�������100�֣���Ϊ���������������ݽ��з���������Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ����֪��ȡ����Ա�гɼ���[50,60)�ڵ�Ƶ��Ϊ3.
����Ա�ijɼ�������100�֣���Ϊ���������������ݽ��з���������Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ����֪��ȡ����Ա�гɼ���[50,60)�ڵ�Ƶ��Ϊ3.

��1����![]() ��ֵ���Ʋ�����Ա��ƽ���ɼ�������С�������λ��Ч���֣���
��ֵ���Ʋ�����Ա��ƽ���ɼ�������С�������λ��Ч���֣���
��2����֪��ȡ��![]() ��������Ա�У��ɼ���[80,90)��[90,100]Ůʿ������Ϊ2�ˣ��ִӳɼ���[80,90)��[90,100]�ij�ȡ����Ա�и������ȡ1�ˣ���������ǡ�ö�ΪŮʿ�ĸ���.
��������Ա�У��ɼ���[80,90)��[90,100]Ůʿ������Ϊ2�ˣ��ִӳɼ���[80,90)��[90,100]�ij�ȡ����Ա�и������ȡ1�ˣ���������ǡ�ö�ΪŮʿ�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() �ϵĵ㵽��������ľ���֮��Ϊ
�ϵĵ㵽��������ľ���֮��Ϊ![]() �����᳤Ϊ
�����᳤Ϊ![]() ��ֱ��
��ֱ��![]() ����ԲC����M��N���㣮
����ԲC����M��N���㣮
��1������ԲC�ķ��̣�
��2����ֱ��![]() ��Բ
��Բ![]() ���У�֤����
���У�֤����![]() Ϊ��ֵ
Ϊ��ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy��,����![]() ��
��![]() =0(a>0)������
=0(a>0)������![]() �IJ�������Ϊ
�IJ�������Ϊ![]() (
(![]() Ϊ����),������ԭ��OΪ����,x��������Ϊ���Ὠ��������ϵ��
Ϊ����),������ԭ��OΪ����,x��������Ϊ���Ὠ��������ϵ��
(1)������![]() ��
��![]() �ļ����귽��;
�ļ����귽��;
(2)��֪�����귽��Ϊ![]() =
=![]() ��ֱ��������
��ֱ��������![]() ��
��![]() �ֱ��ཻ��P��Q���㣨������ԭ��O������|PQ|=
�ֱ��ཻ��P��Q���㣨������ԭ��O������|PQ|=![]() ��1����ʵ��a��ֵ��
��1����ʵ��a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1����![]() ʱ,��
ʱ,��![]() �ĵ����������䣻
�ĵ����������䣻
��2��֤������![]() ʱ��
ʱ��![]() ��������㣻
��������㣻
��3����![]() ������
������![]() ��
��![]() ��ȡ����Сֵ��֤����
��ȡ����Сֵ��֤����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ί.��ί�߶����ӷ�ƶ��������������᳹��ʵ�����ƶ�����ش���߲����ڸ���ƶ����ȫ���ƽ������ƶ�������ȡ���˻�����Ч��ijƶ����Ϊ����Ӧ���Ҿ���ƶ�ĺ��٣��صسа���һ�����أ���֪���ص�ʹ������Լ���Ӧ�Ĺ���ʱ��Ĺ�ϵ���±���ʾ��
����ʹ����� | 1 | 2 | 3 | 4 | 5 |
����ʱ�� | 8 | 10 | 13 | 25 | 24 |
��������ij��300����������������Ը���õ��IJ����������±���ʾ:
Ը�������� | ��Ը�������� | |
���Դ��� | 150 | 50 |
Ů�Դ��� | 50 |
��1��������ϵ��![]() �Ĵ�С�����жϹ���ʱ��
�Ĵ�С�����жϹ���ʱ��![]() ������ʹ�����
������ʹ�����![]() �Ƿ�������أ�
�Ƿ�������أ�
��2���Ƿ���99.9%�İ�����Ϊ������Ա�������������Ը��������ԣ�
��3�����Ըô�Ĵ�����Ա�����������Ը���������ƶ���ص��������Ӹ�ƶ��������ȡ3�ˣ���ȡ����Ը�������������Դ��������Ϊ![]() ,��
,��![]() �ķֲ��м���ѧ������
�ķֲ��м���ѧ������
�ο���ʽ��
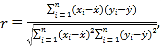
![]()
����![]() ���ٽ�ֵ����
���ٽ�ֵ����
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
�ο����ݣ�![]()
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com