
【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,求
时,求![]() 零点处的切线方程;
零点处的切线方程;
(Ⅱ)若![]() 有两个零点
有两个零点![]() ,求证:
,求证:![]() .
.
【答案】(Ⅰ)![]() 或
或![]() (Ⅱ)见解析
(Ⅱ)见解析
【解析】
(I)先把![]() 代入得到
代入得到![]() ,根据零点存在性原理判断函数的零点坐标原点
,根据零点存在性原理判断函数的零点坐标原点![]() 和
和![]() ,代入求出切线斜率即可求出切线方程;
,代入求出切线斜率即可求出切线方程;
(II)先构造一个函数![]() ,利用这个函数可得到
,利用这个函数可得到![]() ,从而有
,从而有![]() ,再构造
,再构造![]() ,得到
,得到![]() ,有
,有![]() ,再根据
,再根据![]() 即可证明.
即可证明.
解:(Ⅰ)由题意得:![]() ,
,![]() ,定义域为
,定义域为![]() ,
,
![]() ,
,
![]() ,
,![]() 在
在![]() 上为减函数.
上为减函数.
![]() ,
,![]()
![]() 由零点存在定理可知,
由零点存在定理可知,![]() 在
在![]() 上必存在一点
上必存在一点![]() 使
使![]()
![]() 当
当![]() 时,
时,![]() ,即
,即![]() 在
在![]() 上为增函数,
上为增函数,
当![]() 时,
时,![]() ,即
,即![]() 在
在![]() 上为减函数,
上为减函数,
![]() 极大值
极大值![]() ,
,
故![]() 至多有两个零点,又
至多有两个零点,又![]() ,
,![]() ,
,
故![]() ,
,![]() 是
是![]() 的两个零点,
的两个零点,![]() 由
由![]() ,
,![]() ,
,
易得出两切线方程为:![]() 或
或![]()
(Ⅱ)由(Ⅰ)易知![]() ,
,
设![]() ,
,
![]() ,
,![]() ,
,
![]() 在
在![]() 上为增函数,
上为增函数,![]()
![]() 当
当![]() 时,
时,![]() ,即
,即![]() 在
在![]() 上为减函数,
上为减函数,
当![]() 时,
时,![]() ,即
,即![]() 在
在![]() 上为增函数,
上为增函数,
![]() ,即
,即![]() ,
,
设![]() 与
与![]() 的交点横坐标为
的交点横坐标为![]() ,
,
![]() ,
,
![]() 为增函数,
为增函数,![]() ,
,
同理设![]() ,
,
![]() ,
,![]() ,
,
![]() 在
在![]() 上为增函数,
上为增函数,![]() ,
,
![]() 当
当![]() 时,
时,![]() ,即
,即![]() 在
在![]() 上为增函数,
上为增函数,
当![]() 时,
时,![]() ,即
,即![]() 在
在![]() 上为减函数,
上为减函数,
![]() ,即
,即![]() ,
,
设![]() 与
与![]() 的交点横坐标为
的交点横坐标为![]() ,
,
![]() ,
,
![]() 为减函数,
为减函数,![]() ,
,
故:![]() ,
,
![]() 得证.
得证.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】极坐标系中椭圆C的方程为![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴非负半轴,建立平面直角坐标系,且两坐标系取相同的单位长度.
轴非负半轴,建立平面直角坐标系,且两坐标系取相同的单位长度.
(Ⅰ)求该椭圆的直角标方程,若椭圆上任一点坐标为![]() ,求
,求![]() 的取值范围;
的取值范围;
(Ⅱ)若椭圆的两条弦![]() ,
,![]() 交于点
交于点![]() ,且直线
,且直线![]() 与
与![]() 的倾斜角互补,求证:
的倾斜角互补,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高三年级在开学时举行了入学检测.为了了解本年级学生寒假期间历史的学习情况,现从年级![]() 名文科生中随机抽取了
名文科生中随机抽取了![]() 名学生本次考试的历史成绩,得到他们历史分数的频率分布直方图如图.已知本次考试高三年级历史成绩分布区间为
名学生本次考试的历史成绩,得到他们历史分数的频率分布直方图如图.已知本次考试高三年级历史成绩分布区间为![]() .
.

(1)求图中![]() 的值;
的值;
(2)根据频率分布直方图,估计这![]() 名学生历史成绩的平均分,众数;(每组数据用该组的区间中点值作代表)
名学生历史成绩的平均分,众数;(每组数据用该组的区间中点值作代表)
(3)已知该学校每年高考有![]() %的同学历史成绩在一本线以上,用样本估计总体的方法,请你估计本次入学检测历史学科划定的一本线该为多少分?
%的同学历史成绩在一本线以上,用样本估计总体的方法,请你估计本次入学检测历史学科划定的一本线该为多少分?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】笔、墨、纸、砚是中国独有的文书工具,即“文房四宝”.笔、墨、纸、砚之名,起源于南北朝时期,其中的“纸”指的是宣纸,宣纸“始于唐代,产于泾县”,而唐代泾县隶属于宣州府管辖,故因地而得名“宣纸”,宣纸按质量等级,可分为正牌和副牌(优等品和合格品),某公司年产宣纸10000刀(每刀100张),公司按照某种质量标准值![]() 给宣纸确定质量等级,如下表所示:
给宣纸确定质量等级,如下表所示:

公式在所生产的宣纸中随机抽取了一刀(100张)进行检验,得到频率分布直方图如图所示,已知每张正牌纸的利润是10元,副牌纸的利润是5元,废品亏损10元.

(1)估计该公式生产宣纸的年利润(单位:万元);
(2)该公司预备购买一种售价为100万元的机器改进生产工艺,这种机器的使用寿命是一年,只能提高宣纸的质量,不影响产量,这种机器生产的宣纸的质量标准值![]() 的频率,如下表所示:
的频率,如下表所示:
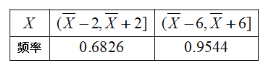
其中![]() 为改进工艺前质量标准值
为改进工艺前质量标准值![]() 的平均值,改进工艺后,每张正牌和副牌宣纸的利润都下降2元,请判断该公司是否应该购买这种机器,并说明理由.
的平均值,改进工艺后,每张正牌和副牌宣纸的利润都下降2元,请判断该公司是否应该购买这种机器,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知点
中,已知点![]() ,
,![]() ,动点
,动点![]() 满足直线
满足直线![]() 与
与![]() 的斜率之积为
的斜率之积为![]() .记
.记![]() 的轨迹为曲线
的轨迹为曲线![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 和
和![]() 的直角坐标方程;
的直角坐标方程;
(2)求![]() 上的点到
上的点到![]() 距离的最小值.
距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,随着“一带一路”倡议的推进,中国与沿线国家旅游合作越来越密切,中国到“一带一路”沿线国家的游客人也越来越多,如图是2013-2018年中国到“一带一路”沿线国家的游客人次情况,则下列说法正确的是( )
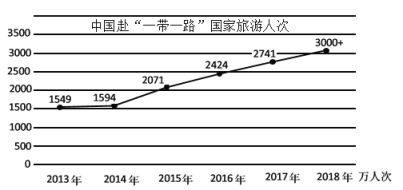
①2013-2018年中国到“一带一路”沿线国家的游客人次逐年增加
②2013-2018年这6年中,2014年中国到“一带一路”沿线国家的游客人次增幅最小
③2016-2018年这3年中,中国到“一带一路”沿线国家的游客人次每年的增幅基本持平
A.①②③B.②③C.①②D.③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知Sn为数列{an}的前n项和,且Sn+2=2an,n∈N*.
(1)求数列{an}的通项公式;
(2)令bn![]() ,设数列{bn}的前项和为Tn,若Tn
,设数列{bn}的前项和为Tn,若Tn![]() ,求n的最小值.
,求n的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2016高考新课标II,理15)有三张卡片,分别写有1和2,1和3,2和3.甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线![]() 的焦点为
的焦点为![]() ,直线
,直线![]() 与抛物线交于
与抛物线交于![]() 两点.
两点.
(1)若![]() 过点
过点![]() ,且
,且![]() ,求
,求![]() 的斜率;
的斜率;
(2)若![]() ,且
,且![]() 的斜率为
的斜率为![]() ,当
,当![]() 时,求
时,求![]() 在
在![]() 轴上的截距的取值范围(用
轴上的截距的取值范围(用![]() 表示),并证明
表示),并证明![]() 的平分线始终与
的平分线始终与![]() 轴平行.
轴平行.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com