
已知集合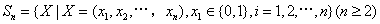 对于
对于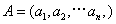 ,
,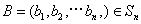 ,定义A与B的差为
,定义A与B的差为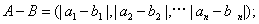 A与B之间的距离为
A与B之间的距离为
(Ⅰ)证明: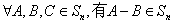 ,且
,且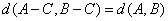 ;
;
(Ⅱ)证明: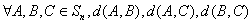 三个数中至少有一个是偶数
三个数中至少有一个是偶数
(Ⅲ) 设P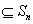 ,P中有m(m≥2)个元素,记P中所有两元素间距离的平均值为
,P中有m(m≥2)个元素,记P中所有两元素间距离的平均值为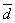 (P).
(P).
证明: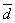 (P)≤
(P)≤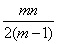 .
.
【分析】:这道题目的难点主要出现在读题上,这里简要分析一下。
题目所给的条件其实包含两个定义,第一个是关于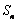 的,其实
的,其实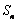 中的元素就是一个n维的坐标,其中每个坐标值都是0或者1,
也可以这样理解,就是一个n位数字的数组,每个数字都只能是0和1, 第二个定义叫距离,距离定义在两者之间,如果直观理解就是看两个数组有多少位不同,因为只有0和1才能产生一个单位的距离,因此这个大题最核心的就是处理数组上的每一位数,然后将处理的结果综合起来,就能看到整体的性质了。
中的元素就是一个n维的坐标,其中每个坐标值都是0或者1,
也可以这样理解,就是一个n位数字的数组,每个数字都只能是0和1, 第二个定义叫距离,距离定义在两者之间,如果直观理解就是看两个数组有多少位不同,因为只有0和1才能产生一个单位的距离,因此这个大题最核心的就是处理数组上的每一位数,然后将处理的结果综合起来,就能看到整体的性质了。
第一问,因为每个数位上都是0或者1,取差的绝对值仍然是0或者1,符合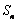 的要求。然后是减去C的数位,不管减去的是0还是1,
每一个a和每一个b都是同时减去的,因此不影响他们原先的差。
的要求。然后是减去C的数位,不管减去的是0还是1,
每一个a和每一个b都是同时减去的,因此不影响他们原先的差。
第二问,先比较A和B有几个不同(因为距离就是不同的有几个),然后比较A和C有几个不同,这两者重复的(就是某一位上A和B不同,A和C不同,那么这一位上B和C就相同)去掉两次(因为在前两次比较中各计算了一次),剩下的就是B和C的不同数目,很容易得到这样的关系式: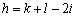 ,从而三者不可能同为奇数。
,从而三者不可能同为奇数。
第三问,首先理解P中会出现 个距离,所以平均距离就是距离总和再除以
个距离,所以平均距离就是距离总和再除以 ,而距离的总和仍然可以分解到每个数位上,第一位一共产生了多少个不同,第二位一共产生了多少个不同,如此下去,直到第n位。然后思考,第一位一共m个数,只有0和1会产生一个单位距离,因此只要分开0和1的数目即可,等算出来
,而距离的总和仍然可以分解到每个数位上,第一位一共产生了多少个不同,第二位一共产生了多少个不同,如此下去,直到第n位。然后思考,第一位一共m个数,只有0和1会产生一个单位距离,因此只要分开0和1的数目即可,等算出来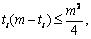 一切就水到渠成了。
一切就水到渠成了。
此外,这个问题需要注意一下数学语言的书写规范。
证明:(Ⅰ)设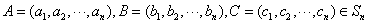
因为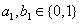 ,所以
,所以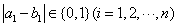
从而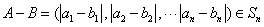
由题意知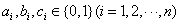 [来源:Zxxk.Com]
[来源:Zxxk.Com]
当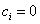 时,
时,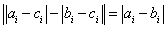
当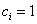 时,
时,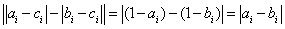
所以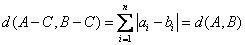
(Ⅱ)设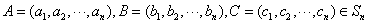
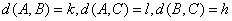
记 由(Ⅱ)可知
由(Ⅱ)可知
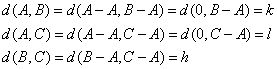
所以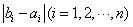 中1的个数为k,
中1的个数为k,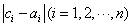 中1的个数为
中1的个数为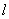
设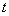 是使
是使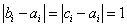 成立的
成立的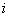 的个数。则
的个数。则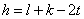
由此可知,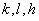 三个数不可能都是奇数
三个数不可能都是奇数
即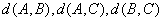 三个数中至少有一个是偶数。
三个数中至少有一个是偶数。
(Ⅲ)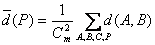 ,其中
,其中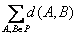 表示P中所有两个元素间距离的总和,设P中所有元素的第
表示P中所有两个元素间距离的总和,设P中所有元素的第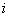 个位置的数字中共有
个位置的数字中共有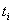 个1,
个1,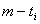 个0,
个0,
则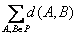
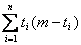
由于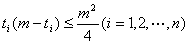
所以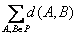
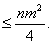
从而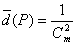
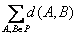
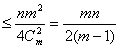


科目:高中数学 来源:2010年高考试题分项版文科数学之专题十五 推理与证明 题型:解答题
(本小题共13分)
已知集合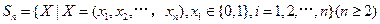 对于
对于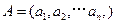 ,
,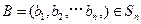 ,定义A与B的差为
,定义A与B的差为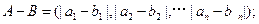
A与B之间的距离为
(Ⅰ)当n=5时,设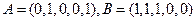 ,求
,求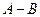 ,
,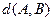 ;
;
(Ⅱ)证明: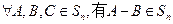 ,且
,且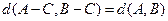 ;
;
(Ⅲ) 证明: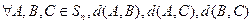 三个数中至少有一个是偶数
三个数中至少有一个是偶数
查看答案和解析>>
科目:高中数学 来源:2010年高考试题分项版理科数学之专题一 集合与简易逻辑 题型:解答题
(本小题共13分)
已知集合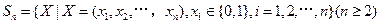 对于
对于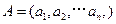 ,
,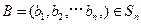 ,定义A与B的差为
,定义A与B的差为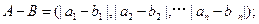
A与B之间的距离为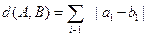
(Ⅰ)证明: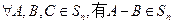 ,且
,且 ;
;
(Ⅱ)证明: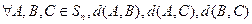 三个数中至少有一个是偶数
三个数中至少有一个是偶数
(Ⅲ) 设P ,P中有m(m≥2)个元素,记P中所有两元素间距离的平均值为
,P中有m(m≥2)个元素,记P中所有两元素间距离的平均值为 (P).
(P). 证明:
证明: (P)≤
(P)≤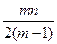 .
.
(考生务必将答案答在答题卡上,在试卷上作答无效)
查看答案和解析>>
科目:高中数学 来源:2010年高考试题(北京卷)解析版(理) 题型:解答题
已知集合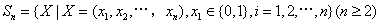 对于
对于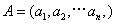 ,
,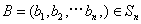 ,定义A与B的差为
,定义A与B的差为
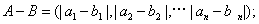
A与B之间的距离为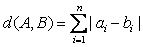
(Ⅰ)证明: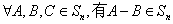 ,且
,且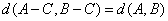 ;
;
(Ⅱ)证明: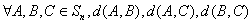 三个数中至少有一个是偶数
三个数中至少有一个是偶数
(Ⅲ) 设P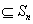 ,P中有m(m≥2)个元素,记P中所有两元素间距离的平均值为
,P中有m(m≥2)个元素,记P中所有两元素间距离的平均值为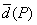 .
.
证明: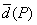 ≤
≤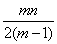 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题共13分)
已知集合![]() 对于
对于![]() ,
,![]() ,定义A与B的差为
,定义A与B的差为
![]()
A与B之间的距离为![]()
(Ⅰ)证明:![]() ,且
,且![]() ;
;
(Ⅱ)证明:![]() 三个数中至少有一个是偶数
三个数中至少有一个是偶数
(Ⅲ) 设P![]() ,P中有m(m≥2)个元素,记P中所有两元素间距离的平均值为
,P中有m(m≥2)个元素,记P中所有两元素间距离的平均值为![]() .
.
证明:![]() ≤
≤![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com