
ΓΨΧβΡΩΓΩ―ß–Θ¥”≤ΈΦ”ΗΏΕΰΡξΦΕΤΎΡ©ΩΦ ‘ΒΡ―ß…ζ÷–≥ι≥ω“Μ–©―ß…ζΘ§≤ΔΆ≥ΦΤΝΥΥϊΟ«ΒΡ ΐ―ß≥…Φ®Θ®≥…Φ®ΨυΈΣ’ϊ ΐ«“¬ζΖ÷ΈΣ100Ζ÷Θ©Θ§ΥυΒΟ ΐΨί’ϊάμΚσΘ§Ν–≥ωΝΥ»γœ¬ΤΒ¬ Ζ÷≤Φ±μΘ°
Ζ÷Ήι | ΤΒ ΐ | ΤΒ¬ |
[40Θ§50Θ© | A | 0.04 |
[50Θ§60Θ© | 4 | 0.08 |
[60Θ§70Θ© | 20 | 0.40 |
[70Θ§80Θ© | 15 | 0.30 |
[80Θ§90Θ© | 7 | B |
[90Θ§100] | 2 | 0.04 |
ΚœΦΤ | C | 1 |

Θ®1Θ©‘ΎΗχ≥ωΒΡ―υ±ΨΤΒ¬ Ζ÷≤Φ±μ÷–Θ§«σAΘ§BΘ§CΒΡ÷ΒΘΜ
Θ®2Θ©≤Ι»ΪΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ§≤Δάϊ”ΟΥϋΙάΦΤ»ΪΧεΗΏΕΰΡξΦΕ―ß…ζΤΎΡ© ΐ―ß≥…Φ®ΒΡ÷Ύ ΐΓΔ÷–ΈΜ ΐΘΜ
Θ®3Θ©œ÷¥”Ζ÷ ΐ‘Ύ[80Θ§90Θ©Θ§[90Θ§100]ΒΡ9ΟϊΆ§―ß÷–ΥφΜζ≥ι»ΓΝΫΟϊΆ§―ßΘ§«σ±Μ≥ι»ΓΒΡΝΫΟϊ―ß…ζΖ÷ ΐΨυ≤ΜΒΆ”Ύ90Ζ÷ΒΡΗ≈¬ Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©2Θ§0.14Θ§50Θ®2Θ©65Θ§ 69.5Θ®3Θ©![]() Θ°
Θ°
ΓΨΫβΈωΓΩ
(1)άϊ”ΟΤΒ¬ Ζ÷≤Φ±μ,ΫαΚœΤΒ¬ ,÷±Ϋ”«σ≥ω![]() ,
,![]() ,
,![]() ΒΡ÷Β;
ΒΡ÷Β;
(2)«σ≥ω÷Ύ ΐ,÷–ΈΜ ΐ,Μ≠≥ωΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΦ¥Ω…;
(3)άϊ”ΟΙ≈ΒδΗ≈–ΆΗ≈¬ ΒΡ«σΖ®,«σΫβΗ≈¬ Φ¥Ω….
(1)![]() ;
;
(2)÷Ύ ΐΈΣΉνΗΏΒΡ–ΓΨΊ–Έ«χΦδ÷–Βψ65,
÷–ΈΜ ΐΈΣ![]() ,
,
ΤΒ¬ ÷±ΖΫΆΦ»γœ¬:

(3)…ηΠΗ={¥”Ζ÷ ΐ‘Ύ[80,100]ΒΡ10ΟϊΆ§―ß÷–ΥφΜζ≥ι»ΓΝΫΟϊΆ§―ß},
![]() ,
,
A={ΝΫΟϊ―ß…ζΖ÷ ΐΨυ≤ΜΒΆ”Ύ90Ζ÷},n(A)=1,
ΗυΨίΙ≈ΒδΗ≈–ΆΦΤΥψΙΪ ΫΩ…ΒΟ .
.


 ΜΤΗ‘¥¥”≈ΨμœΒΝ–¥πΑΗ
ΜΤΗ‘¥¥”≈ΨμœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥–ΘΉι÷·ΒΡ“Μ¥ΈΫΧ Π’–ΤΗΙ≤Ζ÷± ‘ΚΆΟφ ‘ΝΫΗωΜΖΫΎΘ§± ‘ΜΖΫΎΙ≤”–20Οϊ¥σ―ß±œ“Β…ζ≤ΈΦ”Θ§Τδ÷–Ρ–ΓΔ≈°…ζΒΡ±»άΐ«ΓΚΟΈΣ![]() Θ§Τδ≥…Φ®ΒΡΨΞ“ΕΆΦ»γΆΦΥυ Ψ.ΦΌ…η≥…Φ®‘Ύ90Ζ÷“‘…œΒΡΩΦ…ζΩ…“‘Ϋχ»κΟφ ‘ΜΖΫΎ.
Θ§Τδ≥…Φ®ΒΡΨΞ“ΕΆΦ»γΆΦΥυ Ψ.ΦΌ…η≥…Φ®‘Ύ90Ζ÷“‘…œΒΡΩΦ…ζΩ…“‘Ϋχ»κΟφ ‘ΜΖΫΎ.
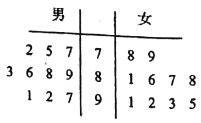
Θ®1Θ© ‘±»ΫœΡ–ΓΔ≈°ΝΫΉι≥…Φ®ΤΫΨυΖ÷ΒΡ¥σ–ΓΘ§≤Δ«σ≥ω≈°…ζΉιΒΡΖΫ≤νΘΜ
Θ®2Θ©¥”Ρ–ΓΔ≈°ΝΫΉιΩ…“‘Ϋχ»κΟφ ‘ΜΖΫΎΒΡΩΦ…ζ÷–Ζ÷±π»Έ»Γ1»ΥΘ§«σΝΫ»ΥΖ÷≤ν≤Μ–Γ”Ύ3Ζ÷ΒΡΗ≈¬ .
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ“‘![]() ΈΣΕΞΒψΒΡΈεΟφΧε÷–Θ§Οφ
ΈΣΕΞΒψΒΡΈεΟφΧε÷–Θ§Οφ![]() ΈΣ’ΐΖΫ–ΈΘ§
ΈΣ’ΐΖΫ–ΈΘ§![]() Θ§
Θ§![]() Θ§«“ΕΰΟφΫ«
Θ§«“ΕΰΟφΫ«![]() ”κΕΰΟφΫ«
”κΕΰΟφΫ«![]() ΕΦ «
ΕΦ «![]() .
.

Θ®1Θ©÷ΛΟςΘΚ![]() ΤΫΟφ
ΤΫΟφ![]() ΘΜ
ΘΜ
Θ®2Θ©«σ÷±œΏ![]() ”κΤΫΟφ
”κΤΫΟφ![]() Υυ≥…Ϋ«ΒΡ’ΐœ“÷Β.
Υυ≥…Ϋ«ΒΡ’ΐœ“÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΦΉ““ΝΫ»ΥΗςΉ‘ΕάΝΔΒΡ≤ΈΦ”Ρ≥ΒΞΈΜΟφ ‘Θ§ΙφΕ®ΟΩΈΜΩΦ…ζ–η“Σ¥”±ύΚ≈ΈΣ1-6ΒΡ6ΒάΟφ ‘Χβ÷–ΥφΜζ≥ι≥ω3ΒάΫχ––Οφ ‘Θ§÷Ν…Ό¥πΕ‘ΝΫΒά≤≈ΡήΚœΗώΘ°“―÷ΣΦΉΡή¥πΕ‘Τδ÷–3ΒάΧβΘ§““Ρή¥πΕ‘Τδ÷–4ΒάΧβΘ°
Θ®1Θ©«σΦΉ«ΓΚΟ¥πΕ‘ΝΫΒάΧβΒΡΗ≈¬ Θ°
Θ®2Θ©«σΦΉΚœΗώ«“““≤ΜΚœΗώΒΡΗ≈¬ Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ÷Ί«λ“Μ÷–ΫΪ“ΣΨΌ–––Θ‘ΑΗη ÷¥σ»ϋΘ§œ÷”–3Ρ–3≈°≤ΈΦ”Θ§–η“ΣΑ≤≈≈ΥϊΟ«ΒΡ≥ω≥ΓΥ≥–ρΘ°Θ®ΫαΙϊ”Ο ΐΉ÷Ής¥πΘ©
Θ®1Θ©»γΙϊ3Ηω≈°…ζΕΦ≤ΜœύΝΎΘ§Ρ«Ο¥”–Εύ…Ό÷÷≤ΜΆ§ΒΡ≥ω≥ΓΥ≥–ρΘΩ
Θ®2Θ©»γΙϊ≈°…ζΦΉ‘Ύ≈°…ζ““ΒΡ«ΑΟφΘ®Ω…“‘≤ΜœύΝΎΘ©Θ§Ρ«Ο¥”–Εύ…Ό÷÷≤ΜΆ§ΒΡ≥ω≥ΓΥ≥–ρΘΩ
Θ®3Θ©»γΙϊ3ΈΜΡ–…ζΕΦœύΝΎΘ§«“≈°…ζΦΉ≤Μ‘ΎΒΎ“ΜΗω≥ω≥ΓΘ§Ρ«Ο¥”–Εύ…Ό÷÷≤ΜΆ§ΒΡ≥ω≥ΓΥ≥–ρΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈ“ΙζΙ≈¥ζ ΐ―ßΉ®÷χΓΕΨ≈’¬Υψ θΓΖ÷–”–“ΜΗωΓΑΝΫ σ¥©«ΫΧβΓ±Θ§ΤδΡΎ»ίΈΣΘΚΓΑΫώ”–‘ΪΚώΈε≥ΏΘ§ΝΫ σΕ‘¥©Θ§¥σ σ»’“Μ≥ΏΘ§–Γ σ“≤»’“Μ≥ΏΘ§¥σ σ»’Ή‘±ΕΘ§–Γ σ»’Ή‘ΑκΘ°Έ ΚΈ»’œύΖξΘΩΗς¥©ΦΗΚΈΘΩΓ±»γΆΦΒΡ≥Χ–ρΩρΆΦ‘¥”Ύ’βΗωΧβΡΩΘ§÷¥––ΗΟ≥Χ–ρΩρΆΦΘ§»τ δ»κx=20Θ§‘ρ δ≥ωΒΡΫαΙϊΈΣΘ®ΓΓΓΓΘ©

A. 3B. 4C. 5D. 6
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐfΘ®xΘ©=ex-mΘ®x+1Θ©+1Θ®mΓ RΘ©Θ°
Θ®1Θ©»τΚ· ΐfΘ®xΘ©ΒΡΦΪ–Γ÷ΒΈΣ1Θ§«σ Β ΐmΒΡ÷ΒΘΜ
Θ®2Θ©Β±xΓί0 ±Θ§≤ΜΒ» Ϋ![]() Κψ≥…ΝΔΘ§«σ Β ΐmΒΡ»Γ÷ΒΖΕΈßΘ°
Κψ≥…ΝΔΘ§«σ Β ΐmΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»τΕ·ΒψPΒΫΒψFΘ®0Θ§1Θ©ΒΡΨύάκ±»ΥϋΒΫ÷±œΏyΘΫ©¹2ΒΡΨύάκ…Ό1Θ§‘ρΕ·ΒψPΒΡΙλΦΘCΒΡΖΫ≥ΧΈΣ_____Θ§»τΙΐΒψΘ®2Θ§1Θ©ΉςΗΟ«ζœΏCΒΡ«–œΏlΘ§‘ρ«–œΏlΒΡΖΫ≥ΧΈΣ_____
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΥΡάβΉΕ![]() ÷–Θ§ΒΉΟφ
÷–Θ§ΒΉΟφ![]() ΈΣΝβ–ΈΘ§÷±œΏ
ΈΣΝβ–ΈΘ§÷±œΏ![]() ΤΫΟφ
ΤΫΟφ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() «
«![]() …œΒΡ“ΜΒψΘ§
…œΒΡ“ΜΒψΘ§![]() .
.

Θ®1Θ©÷ΛΟςΘΚ÷±œΏ![]() ΤΫΟφ
ΤΫΟφ![]() ΘΜ
ΘΜ
Θ®2Θ©»τ![]() Θ§«σΕΰΟφΫ«
Θ§«σΕΰΟφΫ«![]() ΒΡ”ύœ“÷Β.
ΒΡ”ύœ“÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com