
在正四棱柱 中,
中, ,
,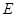 为
为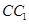 的中点.
的中点.
求证:(I) ∥平面
∥平面 ; (II)
; (II)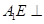 平面
平面 ;
;
(自编)(Ⅲ)若E为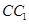 上的动点,试确定
上的动点,试确定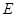 点的位置使直线
点的位置使直线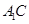 与平面
与平面 所成角的余弦值是
所成角的余弦值是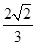 .
.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:高中数学 来源: 题型:
(2009重庆卷文)在正四棱柱![]() 中,顶点
中,顶点![]() 到对角线
到对角线![]() 和到平面
和到平面![]() 的距离分别为
的距离分别为![]() 和
和![]() ,则下列命题中正确的是( )
,则下列命题中正确的是( )
A.若侧棱的长小于底面的变长,则![]() 的取值范围为
的取值范围为![]()
B.若侧棱的长小于底面的变长,则![]() 的取值范围为
的取值范围为![]()
C.若侧棱的长大于底面的变长,则![]() 的取值范围为
的取值范围为![]()
D.若侧棱的长大于底面的变长,则![]() 的取值范围为
的取值范围为![]()
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省莱芜市高三4月自主检测文科数学试卷(解析版) 题型:解答题
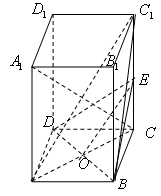
如图,在正四棱柱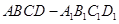 中,
中,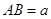 ,
,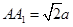 ,
, 为
为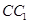 的中点,
的中点,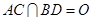 .
.
(Ⅰ) 证明: ∥平面
∥平面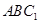 ;
;
(Ⅱ)证明: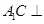 平面
平面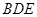 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知正四棱柱![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 为直线
为直线![]() 上的动点,设
上的动点,设![]() .
.

(1)当![]() 时,求
时,求![]() 与平面
与平面![]() 所成的角;
所成的角;
(2)当![]() 时,求二面角
时,求二面角![]() 的大小(用反三角函数表示);
的大小(用反三角函数表示);
(3)在(2)的条件下,求![]() 点到平面
点到平面![]() 的距离。
的距离。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com