
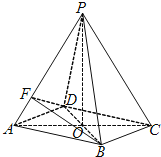
【题目】如图所示,在四棱锥![]() 中,底面四边形ABCD是菱形,
中,底面四边形ABCD是菱形, ![]() 是边长为2的等边三角形,
是边长为2的等边三角形, ![]() ,
, ![]() .
.
![]() Ⅰ
Ⅰ![]() 求证:
求证: ![]() 底面ABCD;
底面ABCD;
![]() Ⅱ
Ⅱ![]() 求直线CP与平面BDF所成角的大小;
求直线CP与平面BDF所成角的大小;
![]() Ⅲ
Ⅲ![]() 在线段PB上是否存在一点M,使得
在线段PB上是否存在一点M,使得![]() 平面BDF?如果存在,求
平面BDF?如果存在,求![]() 的值,如果不存在,请说明理由.
的值,如果不存在,请说明理由.
【答案】![]() Ⅰ
Ⅰ![]() 见解析;
见解析; ![]() Ⅱ
Ⅱ![]() Ⅲ
Ⅲ![]() .
.
【解析】试题分析:
(Ⅰ) 由题意可得![]() ,从而可得
,从而可得![]() 底面ABCD. (Ⅱ)建立空间直角坐标系,利用坐标法求解即可得到所求的线面角.
底面ABCD. (Ⅱ)建立空间直角坐标系,利用坐标法求解即可得到所求的线面角. ![]() Ⅲ
Ⅲ![]() 根据坐标法求解探索性问题,假设存在点M满足条件,并设且
根据坐标法求解探索性问题,假设存在点M满足条件,并设且![]() ,求得点点M坐标后,根据
,求得点点M坐标后,根据![]() 与平面BDF的法向量垂直可得
与平面BDF的法向量垂直可得![]() ,从而得到符合题意的点M存在.
,从而得到符合题意的点M存在.
试题解析:
![]() Ⅰ
Ⅰ![]() 证明:∵四边形ABCD是菱形,
证明:∵四边形ABCD是菱形,
∴O为![]() 中点
中点![]()
又![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() 底面
底面![]()
![]() Ⅱ
Ⅱ![]() 解:由底面ABCD是菱形可得
解:由底面ABCD是菱形可得![]() ,又由
,又由![]() Ⅰ
Ⅰ![]() 可知
可知![]() .
.
建立如图所示的空间直角坐标系![]() .
.

由![]() 是边长为2的等边三角形,
是边长为2的等边三角形, ![]() ,可得
,可得![]() .
.
所以![]()
∴![]()
![]() .
.
由已知可得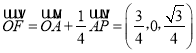 ,
,
设平面BDF的法向量为![]() ,
,
由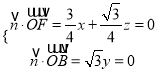 ,可得
,可得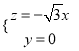 ,
,
令![]() ,则
,则![]() .
.
设直线CP与平面BDF所成的角为![]() ,
,
则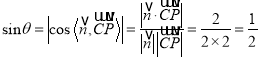 ,
,
又![]() ,
,
∴![]() .
.
∴直线CP与平面BDF所成角的大小为![]() .
.
![]() Ⅲ
Ⅲ![]() 解:假设存在点M满足条件,且
解:假设存在点M满足条件,且![]() ,
,
则![]() .
.
若使![]() 平面BDF,需且仅需
平面BDF,需且仅需![]() 且
且![]()
![]() 平面BDF,
平面BDF,
由![]() ,解得
,解得![]() 符合题意.
符合题意.
∴在线段PB上存在一点M,使得![]() 平面BDF,且
平面BDF,且![]()


科目:高中数学 来源: 题型:
【题目】如图,△ABC是直角三角形,∠ABC=90°,以AB为直径的圆O交AC于点E,点D是BC边的中点,连接OD交圆O于点M. 
(1)求证:O、B、D、E四点共圆;
(2)求证:2DE2=DMAC+DMAB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校课题组为了研究学生的数学成绩和物理成绩之间的关系,随机抽取高二年级20名学生某次考试成绩(百分制)如表所示:
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
数学成绩 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 83 | 72 | 83 |
物理成绩 | 90 | 63 | 72 | 87 | 91 | 71 | 58 | 82 | 93 | 81 | 77 | 82 | 48 | 85 | 69 | 91 | 61 | 84 | 78 | 86 |
若数学成绩90分(含90分)以上为优秀,物理成绩85(含85分)以上为优秀.有多少把握认为学生的数学成绩与物理成绩之间有关系( )
A.99.5%
B.99.9%
C.97.5%
D.95%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,直角梯形ABCD中,∠ABC=90°,AB=BC=2AD=4,点E、F分别是AB、CD的中点,点G在EF上,沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF,如图2.
(1)当AG+GC最小时,求证:BD⊥CG;
(2)当2VB﹣ADGE=VD﹣GBCF时,求二面角D﹣BG﹣C平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)满足对任意的m,n都有f(m+n)=f(m)+f(n)-1,设g(x)=f(x)+![]() (a>0,a≠1),g(ln2018)=-2015,则g(ln
(a>0,a≠1),g(ln2018)=-2015,则g(ln![]() )=______.
)=______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,直角梯形
,直角梯形![]() 通过直角梯形
通过直角梯形![]() 以直线
以直线![]() 为轴旋转得到,且使得平面
为轴旋转得到,且使得平面![]() 平面
平面![]() .
. ![]() 为线段
为线段![]() 的中点,
的中点, ![]() 为线段
为线段![]() 上的动点.
上的动点.

(![]() )求证:
)求证: ![]() .
.
(![]() )当点
)当点![]() 满足
满足![]() 时,求证:直线
时,求证:直线![]() 平面
平面![]() .
.
(![]() )当点
)当点![]() 是线段
是线段![]() 中点时,求直线
中点时,求直线![]() 和平面
和平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A、B、C所对的边分别为a、b、c,f (x)=sin(2x﹣A) (x∈R),函数f(x)的图象关于点( ![]() ,0)对称.
,0)对称.
(1)当x∈(0, ![]() )时,求f (x)的值域;
)时,求f (x)的值域;
(2)若a=7且sinB+sinC= ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司采用招考方式引进人才,规定必须在![]() ,三个测试点中任意选取两个进行测试,若在这两个测试点都测试合格,则可参加面试,否则不被录用,已知考生在每测试个点测试结果互不影响,若考生小李和小王一起前来参加招考,小李在测试点
,三个测试点中任意选取两个进行测试,若在这两个测试点都测试合格,则可参加面试,否则不被录用,已知考生在每测试个点测试结果互不影响,若考生小李和小王一起前来参加招考,小李在测试点![]() 测试合格的概率分别为
测试合格的概率分别为![]() ,小王在上述三个测试点测试合格的概率都是
,小王在上述三个测试点测试合格的概率都是![]() .
.
(1)问小李选择哪两个测试点测试才能使得可以参加面试的可能性最大?请说明理由;
(2)假设小李选择测试点![]() 进行测试,小王选择测试点
进行测试,小王选择测试点![]() 进行测试,记
进行测试,记![]() 为两人在各测试点测试合格的测试点个数之和,求随机变量
为两人在各测试点测试合格的测试点个数之和,求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com