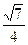[方法一]:(几何法)
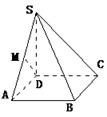
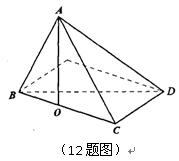
(I)证法一:如图1,∵底面ABCD是正方形, ∴BC⊥DC.
∵SD⊥底面ABCD,∴DC是SC在平面ABCD上的射影,
由三垂线定理得BC⊥SC.…………3分
证法二:如图1,∵底面ABCD是正方形, ∴BC⊥DC.
∵SD⊥底面ABCD,∴SD⊥BC,又DC∩SD=D, 图1
∴BC⊥平面SDC,∴BC⊥SC.…………3分
(II)解法一:∵SD⊥底面ABCD,且ABCD为正方形,
∴可把四棱锥S—ABCD补形为长方体A
1B
1C
1S—ABCD,
如图2,面ASD与面BSC所成的二面角就是面ADSA
1与面BCSA
1所成的二面角,
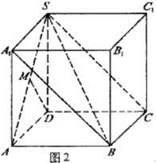
∵SC⊥BC,BC//A
1S,∴SC⊥A
1S,
又SD⊥A
1S,∴∠CSD为所求二面角的平面角.
在Rt△SCB中,由勾股定理得SC=
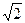
,在Rt△SDC中,
由勾股定理得SD=1.
∴∠CSD=45°.即面ASD与面BSC所成的二面角为45°.……………8分
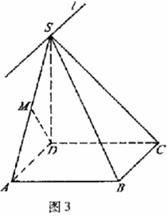
解法二:如图3,过点S作直线
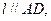
在面ASD上,
∵底面ABCD为正方形,
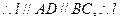
在面BSC上,
为面ASD与面BSC的交线.
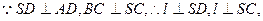
∴∠CSD为面ASD与面BSC所成二面角的平面角.
在Rt△SCB中,由勾股定理得SC=
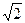
,在Rt△SDC中,
由勾股定理得SD=1.
∴∠CSD=45°.即面ASD与面BSC所成的二面角
为45°。…8分
(III)解法一:如图3,∵SD=AD=1,∠SDA=90°,∴△SDA是等腰直角三角形.
又M是斜边SA的中点, ∴DM⊥SA.
∵BA⊥AD,BA⊥SD,AD∩SD=D,∴BA⊥面ASD,SA是SB在面ASD上的射影.
由三垂线定理得DM⊥SB. ∴异面直线DM与SB所成的角为90°. ……………14分
解法二:如图4,取AB中点P,连结MP,DP.
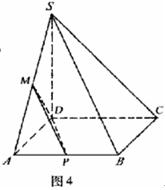
在△ABS中,由中位线定理得 MP//SB,
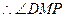
是异面直线DM与SB所成的角.
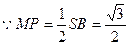
,
又
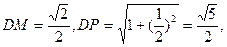
∴在△DMP中,有DP
2=MP
2+DM
2,
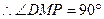
即异面直线DM与SB所成的角为90°. ……………14分
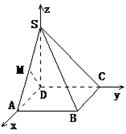
[方法二]:(向量法)
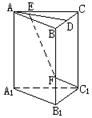
解析:如图所示,以D为坐标原点建立直角坐标系,
则D(0,0,0),A(1,0,0),B(1,1,0),C(0,1,0),
M(
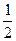
,0,
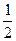
),
∵ SB=
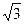
,DB=
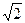
,SD=1,∴ S(0,0,1),……………2分
(I)证明:∵
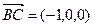
,
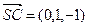
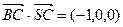
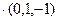
="0 " ∴
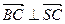
,即BC
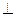
SC.……………5分
(II)设二面角的平面角为
θ,由题意可知平面ASD的一个法向量为
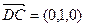
,设平面BSC的法向量为
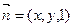
,由
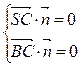
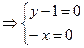
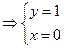
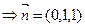
,
得
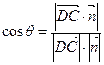
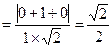
,
∴ 面ASD与面BSC所成的二面角为45°.……………10分
(III)设异面直线DM与SB所成角为α,

∵
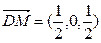
,SB=(-1,-1,1),得
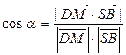
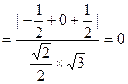
∴ 异面直线DM与SB所成角为90°.……………14分


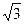 .
. SC;
SC; (I)证法一:如图1,∵底面ABCD是正方形, ∴BC⊥DC.
(I)证法一:如图1,∵底面ABCD是正方形, ∴BC⊥DC. ∵SC⊥BC,BC//A1S,∴SC⊥A1S,
∵SC⊥BC,BC//A1S,∴SC⊥A1S,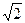 ,在Rt△SDC中,
,在Rt△SDC中,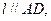
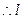 在面ASD上,
在面ASD上, ∵底面ABCD为正方形,
∵底面ABCD为正方形,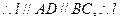 在面BSC上,
在面BSC上,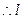 为面ASD与面BSC的交线.
为面ASD与面BSC的交线.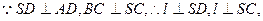
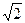 ,在Rt△SDC中,
,在Rt△SDC中, 在△ABS中,由中位线定理得 MP//SB,
在△ABS中,由中位线定理得 MP//SB,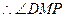 是异面直线DM与SB所成的角.
是异面直线DM与SB所成的角.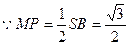 ,
,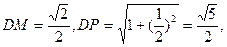
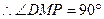
 [方法二]:(向量法)
[方法二]:(向量法)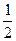 ,0,
,0,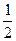 ),
),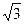 ,DB=
,DB=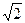 ,SD=1,∴ S(0,0,1),……………2分
,SD=1,∴ S(0,0,1),……………2分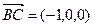 ,
,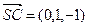
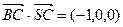
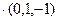 ="0 " ∴
="0 " ∴ 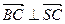 ,即BC
,即BC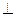 SC.……………5分
SC.……………5分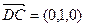 ,设平面BSC的法向量为
,设平面BSC的法向量为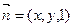 ,由
,由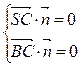
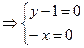
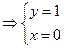
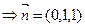 ,
,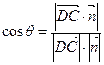
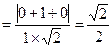 ,
, ∵
∵ 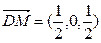 ,SB=(-1,-1,1),得
,SB=(-1,-1,1),得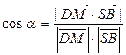
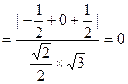



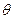 ,则sin
,则sin