
分析 (1)利用椭圆的定义及其三角形三边大小关系可得:|PA|+|PF2|=2a+|PA|-|PF1|≤≤2a+|AF1|=2a+$\sqrt{2}$ (当p为AF1延长线与椭圆交点时取等号),即可得出.
(2)当直线MN的斜率存在时,设直线MN的方程为y=k(x-1),与椭圆方程联立可得(3+4k2)x2-8k2x+4k2-12=0.设点R(x,y),由$\overrightarrow{{F}_{1}M}$+$\overrightarrow{{F}_{2}M}$=$\overrightarrow{{F}_{1}R}$,利用根与系数的关系可得:x-1=$\frac{8{k}^{2}}{3+4{k}^{2}}$,y=$\frac{-6k}{3+4{k}^{2}}$.消去k后即可得出,当直线MN的斜率不存在时,验证即可.
(3)设△F1MN的内切圆的半径为R,则△F1MN的周长=4a,${S}_{△{F}_{1}MN}$=4R.因此${S}_{△{F}_{1}MN}$最大,R就最大,又${S}_{△{F}_{1}MN}$=$\frac{1}{2}|{F}_{1}{F}_{2}|$|y1-y2|=|y1-y2|,由题意知,直线l的斜率不为零,可设直线l的方程为x=my+1,与椭圆方程联立化为(3m2+4)y2+6my-9=0,利用根与系数的关系可得:${S}_{△{F}_{1}MN}$=|y1-y2|=$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$,通过换元求导即可得出其最大值.
解答 解:(1)∵|PA|+|PF2|=2a+|PA|-|PF1|,
∴|PA|+|PF2|≤2a+|AF1|=2a+$\sqrt{2}$ (当p为AF1延长线与椭圆交点时取等号).
∴2a+$\sqrt{2}$=4+$\sqrt{2}$,
解得a=2,
∴椭圆C1:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1.
(2)当直线MN的斜率存在时,设直线MN的方程为y=k(x-1),
由$\left\{\begin{array}{l}{y=k(x-1)}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,消去y,得(3+4k2)x2-8k2x+4k2-12=0.
∴x1+x2=$\frac{8{k}^{2}}{3+4{k}^{2}}$,y1+y2=k(x1+x2)-2k=$\frac{-6k}{3+4{k}^{2}}$.
设点R(x,y),
∵$\overrightarrow{{F}_{1}M}$=(x1+1,y1),$\overrightarrow{{F}_{1}N}$=(x2+1,y2),$\overrightarrow{{F}_{1}R}$=(x+1,y).
∵$\overrightarrow{{F}_{1}M}$+$\overrightarrow{{F}_{2}M}$=$\overrightarrow{{F}_{1}R}$,
∴x1+x2+2=x+1,y1+y2=y.
∴x-1=$\frac{8{k}^{2}}{3+4{k}^{2}}$,y=$\frac{-6k}{3+4{k}^{2}}$.
消去k后,化简得4y2+3(x-2)2=3(x≠3),
即$(x-2)^{2}+\frac{{y}^{2}}{\frac{3}{4}}$=1(x≠3).
当直线MN的斜率不存在时,设直线MN的方程为:x=-1.,
依题意,可得点R(3,0),经检验,点R在曲线$(x-2)^{2}+\frac{{y}^{2}}{\frac{3}{4}}$=1上.
∴动点R的轨迹方程为即$(x-2)^{2}+\frac{{y}^{2}}{\frac{3}{4}}$=1.
(3)设△F1MN的内切圆的半径为R,
则△F1MN的周长=4a=8,${S}_{△{F}_{1}MN}$=$\frac{1}{2}$×8R=4R.
因此${S}_{△{F}_{1}MN}$最大,R就最大,又${S}_{△{F}_{1}MN}$=$\frac{1}{2}|{F}_{1}{F}_{2}|$|y1-y2|=|y1-y2|,
由题意知,直线l的斜率不为零,可设直线l的方程为x=my+1,
联立$\left\{\begin{array}{l}{x=my+1}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,化为(3m2+4)y2+6my-9=0,
△>0成立.
∴y1+y2=$\frac{-6m}{3{m}^{2}+4}$,y1y2=$\frac{-9}{3{m}^{2}+4}$,
则${S}_{△{F}_{1}MN}$=|y1-y2|=$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=$\frac{12\sqrt{{m}^{2}+1}}{3{m}^{2}+4}$,
令t=$\sqrt{{m}^{2}+1}$≥1,
则${S}_{△{F}_{1}MN}$=$\frac{12t}{3{t}^{2}+1}$=$\frac{12}{3t+\frac{1}{t}}$,
令f(t)=3t+$\frac{1}{t}$,f′(t)=3-$\frac{1}{{t}^{2}}$=$\frac{3{t}^{2}-1}{{t}^{2}}$>0,
∴f(t)在[1,+∞)上单调递增,有f(t)≥f(1)=4,
∴${S}_{△{F}_{1}MN}$$≤\frac{12}{4}$=3,
即当t=1,m=0时,${S}_{△{F}_{1}MN}$=取得最大值3,又${S}_{△{F}_{1}MN}$=4R,
∴Rmax=$\frac{3}{4}$,
这时所求内切圆面积的最大值为$\frac{9π}{16}$.
故存在直线l:x=1,使△F1MN的内切圆面积的最大值为$\frac{9π}{16}$.
点评 本题考查了直线与椭圆相交问题、一元二次方程的根与系数的关系、向量坐标运算、三角形面积计算公式、三角形内切圆的面积计算公式、利用导数研究函数单调性极值与最值,考查了推理能力与计算能力,属于难题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
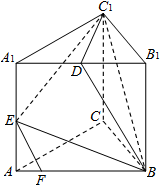 在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥平面ABC,D为棱A1B1的中点,E为AA1的中点,点F在棱AB上,且AF=$\frac{1}{4}$AB.
在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥平面ABC,D为棱A1B1的中点,E为AA1的中点,点F在棱AB上,且AF=$\frac{1}{4}$AB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
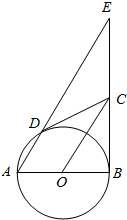 如图,AB为圆O的直径,CB是圆O的切线,弦AD∥OC.
如图,AB为圆O的直径,CB是圆O的切线,弦AD∥OC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
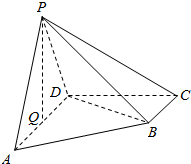 四棱锥P-ABCD中底面ABCD为直角梯形,AD∥BC,∠ADC=90°,面PAD⊥面ABCD,Q为AD的中点,PA=PD=2,AD=2BC=2,CD=$\sqrt{3}$.
四棱锥P-ABCD中底面ABCD为直角梯形,AD∥BC,∠ADC=90°,面PAD⊥面ABCD,Q为AD的中点,PA=PD=2,AD=2BC=2,CD=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 平行 | B. | 垂直 | C. | 重合 | D. | 相交但不垂直 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com