
分析 可设Ai纸张的长度为yi,i=0,1,…,8,由题意可得y4=2$\sqrt{2}$,再由等比数列的通项公式和面积公式,以及求和公式,即可得到所求值.
解答 解:可设Ai纸张的长度为yi,i=0,1,…,8,
由A4纸的宽度为2dm,且纸张的幅宽和长度的比例关系都为$x:y=1:\sqrt{2}$,
可得y4=2$\sqrt{2}$,
由题意可得y0=2$\sqrt{2}$•24=32$\sqrt{2}$,即有A0纸的面积为32$\sqrt{2}$×2=64$\sqrt{2}$dm2;
由A0,A1,A2,…,A8纸9张纸的面积构成一个以64$\sqrt{2}$为首项,$\frac{1}{2}$为公比的等比数列,
可得这9张纸的面积之和为$\frac{64\sqrt{2}(1-\frac{1}{{2}^{9}})}{1-2}$=$\frac{511\sqrt{2}}{4}$dm2.
故答案为:64$\sqrt{2}$,$\frac{511\sqrt{2}}{4}$.
点评 本题考查数列模型的应用题的解法,考查等比数列的通项公式和求和公式的运用,考查运算能力,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 0<x0<$\frac{1}{2}$ | B. | $\frac{1}{2}$<x0<1 | C. | $\frac{\sqrt{2}}{2}$<x0<$\sqrt{2}$ | D. | $\sqrt{2}$<x0$<\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,ex-x-1<0 | B. | ?x0∈R,e${\;}^{{x}_{0}}$-x0-1≤0 | ||
| C. | ?x0∈R,e${\;}^{{x}_{0}}$-x0-1<0 | D. | ?x∈R,ex-x-1≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
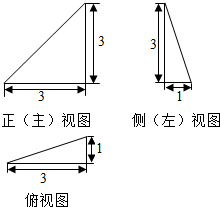
| A. | $\frac{3}{2}$cm3 | B. | 2cm3 | C. | 3cm3 | D. | 9cm3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x-y-3=0 | B. | 2x-y-1=0 | C. | x+2y-1=0 | D. | x+2y-4=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
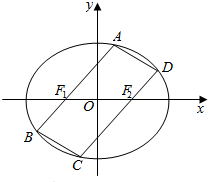 已知椭圆E的中心在坐标原点,左、右焦点F1、F2分别在x轴上,离心率为$\frac{1}{2}$,在其上有一动点A,A到点F1距离的最小值是1,过A、F1作一个平行四边形,顶点A、B、C、D都在椭圆E上,如图所示.
已知椭圆E的中心在坐标原点,左、右焦点F1、F2分别在x轴上,离心率为$\frac{1}{2}$,在其上有一动点A,A到点F1距离的最小值是1,过A、F1作一个平行四边形,顶点A、B、C、D都在椭圆E上,如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com