
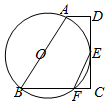
 已知:如图,梯形ABCD中,AD∥BC,∠C=$\frac{π}{2}$,以AB为直径的⊙O恰与CD相切于点E,⊙O交BC于F,连结EF.
已知:如图,梯形ABCD中,AD∥BC,∠C=$\frac{π}{2}$,以AB为直径的⊙O恰与CD相切于点E,⊙O交BC于F,连结EF.分析 (Ⅰ)连接OE,利用圆的直径与梯形的中位线定理,即可证明结论成立;
(Ⅱ)连接AF,利用勾股定理和切割线定理,结合题意即可求出EF是AD与AB的等比中项.
解答  证明:(Ⅰ)如图所示,
证明:(Ⅰ)如图所示,
连接OE,∵CD与⊙O相切于点E,
∴OE=$\frac{1}{2}$AB,
又OE⊥DC,
∠C=$\frac{π}{2}$,
∴OE∥BC,且OE=$\frac{1}{2}$(AD+BC),
∴AD+BC=AB;
(Ⅱ)∵CD与⊙O相切,
∴CE2=CF•CB,
连接AF,则AF⊥BF,
∴AF∥CD,
∴AD=FC,
∴EF2=CE2+CF2
=CF•CB+CF2
=CF•(CB+CF)
=AD•(CB+AD)
=AD•AB;
即EF是AD与AB的等比中项.
点评 本题考查了与圆有关的比例线段以及切割线定理的应用问题,考查了逻辑推理与证明能力,是综合性题目.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 28 | B. | 30 | C. | 36 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,CB=CD=2.面EAD⊥面ABCD,面FCB⊥面ABCD,且CF⊥BC.
如图几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,CB=CD=2.面EAD⊥面ABCD,面FCB⊥面ABCD,且CF⊥BC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图1,在直角梯形ABCD中,AB∥CD,∠DAB=90°,点E、F分别在CD、AB上,且EF⊥CD,BE⊥BC,BC=1,CE=2.现将矩形ADEF沿EF折起,使平面ADEF与平面EFBC垂直(如图2).
如图1,在直角梯形ABCD中,AB∥CD,∠DAB=90°,点E、F分别在CD、AB上,且EF⊥CD,BE⊥BC,BC=1,CE=2.现将矩形ADEF沿EF折起,使平面ADEF与平面EFBC垂直(如图2).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图所示,网格线上正方形的边长为1,粗实线和粗虚线给出的是某几何体的三视图,则该几何体的体积为( )
如图所示,网格线上正方形的边长为1,粗实线和粗虚线给出的是某几何体的三视图,则该几何体的体积为( )| A. | $\frac{11}{2}$ | B. | 6 | C. | $\frac{13}{2}$ | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
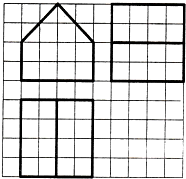 如图,网格纸上每个正方形小格的边长为1,图中粗线画出的是某多面体的三视图,则该几何体的表面积为( )
如图,网格纸上每个正方形小格的边长为1,图中粗线画出的是某多面体的三视图,则该几何体的表面积为( )| A. | $56+16\sqrt{2}$ | B. | 56+8$\sqrt{2}$ | C. | 64 | D. | 72 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,+∞) | B. | (-1,1] | C. | (-∞,1) | D. | [-1,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com