
【题目】已知数列A:a1,a2,…,an(0≤a1<a2<…<an,n≥3)具有性质P:对任意i,j(1≤i≤j≤n),aj+ai与aj-ai两数中至少有一个是该数列中的一项。现给出以下四个结论:
①数列0,1,3具有性质P;
②数列0,2,4,6具有性质P;
③若数列A具有性质P,则a1=0;
④若数列a1,a2,a3(0≤a1<a2<a3)具有性质P,则a1+a3=2a2。
其中正确的结论有( )
A. 4个 B. 3个 C. 2个 D. 1个
科目:高中数学 来源: 题型:
【题目】给出下列判断:①一条直线和一点确定一个平面;②两条直线确定一个平面;③三角形和梯形一定是平面图形;④三条互相平行的直线一定共面其中正确的是_______.(写出所有正确判断的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学举行了一次“环保知识竞赛”活动. 为了了解本次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为![]() )进行统计. 按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在[50,60),[90,100]的数据).
)进行统计. 按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在[50,60),[90,100]的数据).


(1)求样本容量![]() 和频率分布直方图中的
和频率分布直方图中的![]() ,
,![]() 的值;
的值;
(2)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取3名同学到市政广场参加环保知识宣传的志愿者活动,设![]() 表示所抽取的3名同学中得分在[80,90)的学生人数,求
表示所抽取的3名同学中得分在[80,90)的学生人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015年五一节”期间,高速公路车辆“较多,交警部门通过路面监控装置抽样调查某一山区路段汽车行驶速度,采用的方法是:按到达监控点先后顺序,每隔50辆抽取一辆,总共抽取120辆,分别记下其行车速度,将行车速度(km/h)分成七段[60,65),[65,70),[70,75),[75,80),[80,85),[85,90),[90,95)后得到如图所示的频率分布直方图,据图解答下列问题:
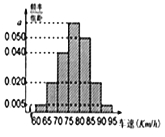
(1)求a的值,并说明交警部门采用的是什么抽样方法?
(2)若该路段的车速达到或超过90km/h即视为超速行驶,求超速行驶的概率
(3)求这120辆车行驶速度的众数和中位数的估计值(精确到0.1)。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中,正确的有__________.(写出所有正确说法的序号)
①已知关于![]() 的不等式
的不等式![]() 的角集为
的角集为![]() ,则实数
,则实数![]() 的取值范围是
的取值范围是![]() .
.
②已知等比数列![]() 的前
的前![]() 项和为
项和为![]() ,则
,则![]() 、
、![]() 、
、![]() 也构成等比数列.
也构成等比数列.
③已知函数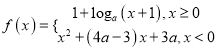 (其中
(其中![]() 且
且![]() )在
)在![]() 上单调递减,且关于
上单调递减,且关于![]() 的方程
的方程![]() 恰有两个不相等的实数解,则
恰有两个不相等的实数解,则![]() .
.
④已知![]() ,且
,且![]() ,则
,则![]() 的最小值为
的最小值为![]() .
.
⑤在平面直角坐标系中, ![]() 为坐标原点,
为坐标原点, ![]() 则
则![]() 的取值范围是
的取值范围是![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的方程是
的方程是![]() ,圆
,圆![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).以原点
为参数).以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)分别求直线![]() 与圆
与圆![]() 的极坐标方程;
的极坐标方程;
(2)射线![]() :
:![]() (
(![]() )与圆
)与圆![]() 的交点为
的交点为![]() 、
、![]() 两点,与直线
两点,与直线![]() 交于点
交于点![]() ,射线
,射线![]() :
:![]() 与圆
与圆![]() 交于
交于![]() ,
,![]() 两点,与直线
两点,与直线![]() 交于点
交于点![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商品进货价每件50元,据市场调查,当销售价格(每件x元)在50≤ x ≤80时,每天售出的件数为P= ,每天获得的利润为y(元)
,每天获得的利润为y(元)
(1)写出关于x的函数y的表达式;
(2)若想每天获得的利润最多,问售价应定为每件多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-1《几何证明选讲》
已知A、B、C、D为圆O上的四点,直线DE为圆O的切线,AC∥DE,AC与BD相交于H点

(1)求证:BD平分∠ABC;
(2)若AB=4,AD=6,BD=8,求AH的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com