
ЁОЬтФПЁПФГЩЬГЁОйаагаНБДйЯњЛюЖЏЃЌЙЫПЭЙКТђвЛЖЈН№ЖюЩЬЦЗКѓМДПЩГщНБЃЌУПДЮГщНБЖМДгзАга4ИіКьЧђЁЂ6ИіАзЧђЕФМзЯфКЭзАга5ИіКьЧђЁЂ5ИіАзЧђЕФввЯфжаЃЌИїЫцЛњУўГі1ИіЧђЃЌдкУўГіЕФ2ИіЧђжаЃЌШєЖМЪЧКьЧђЃЌдђЛёвЛЕШНБЃЛШєжЛга1ИіКьЧђЃЌдђЛёЖўЕШНБЃЛШєУЛгаКьЧђЃЌдђВЛЛёНБ.
ЃЈ1ЃЉЧѓЙЫПЭГщНБ1ДЮФмЛёНБЕФИХТЪЃЛ
ЃЈ2ЃЉШєФГЙЫПЭга3ДЮГщНБЛњЛсЃЌМЧИУЙЫПЭдк3ДЮГщНБжаЛёвЛЕШНБЕФДЮЪ§ЮЊxЃЌЧѓxЕФЗжВМСаКЭЪ§бЇЦкЭћ.
ЁОД№АИЁП
ЃЈ1ЃЉНтЃКМЧЪТМў ![]() ЃћДгМзЯфжаУўГіЕФ1ИіЧђЪЧКьЧђЃ§ЃЌ
ЃћДгМзЯфжаУўГіЕФ1ИіЧђЪЧКьЧђЃ§ЃЌ ![]() ЃћДгввЯфжаУўГіЕФ1ИіЧђЪЧКьЧђЃ§
ЃћДгввЯфжаУўГіЕФ1ИіЧђЪЧКьЧђЃ§
![]() ЃћЙЫПЭГщНБ1ДЮЛёвЛЕШНБЃ§ЃЌ
ЃћЙЫПЭГщНБ1ДЮЛёвЛЕШНБЃ§ЃЌ ![]() ЃћЙЫПЭГщНБ1ДЮЛёЖўЕШНБЃ§ЃЌ
ЃћЙЫПЭГщНБ1ДЮЛёЖўЕШНБЃ§ЃЌ ![]() ЃћЙЫПЭГщНБ1ДЮФмЛёНБЃ§ЃЌгЩЬтвтЃЌ
ЃћЙЫПЭГщНБ1ДЮФмЛёНБЃ§ЃЌгЩЬтвтЃЌ ![]() гы
гы ![]() ЯрЛЅЖРСЂЃЌ
ЯрЛЅЖРСЂЃЌ ![]() гы
гы ![]() ЛЅГтЃЌ
ЛЅГтЃЌ ![]() гы
гы ![]() ЛЅГтЃЌЧв
ЛЅГтЃЌЧв ![]()
![]() ЃЌ
ЃЌ ![]()
![]()
![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ
Ёп ![]() ЃЌ
ЃЌ ![]() ЃЌЁр
ЃЌЁр ![]() ЃЌ
ЃЌ

![]() ЃЌ
ЃЌ
ЙЪЫљЧѓИХТЪЮЊ ![]()
ЃЈ2ЃЉНтЃКЙЫПЭГщНБ3ДЮЖРСЂжиИДЪдбщЃЌгЩЃЈ1ЃЉжЊЃЌЙЫПЭГщНБ1ДЮЛёвЛЕШНБЕФИХТЪЮЊ ![]() ЃЌЁр
ЃЌЁр ![]() ЃЌ
ЃЌ
гкЪЧ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ
![]() ЃЌЙЪxЕФЗжВМСаЮЊ
ЃЌЙЪxЕФЗжВМСаЮЊ
x | 0 | 1 | 2 | 3 |
p |
|
|
|
|
xЕФЪ§бЇЦкЭћЮЊ ![]() .
.
ЁОНтЮіЁПЃЈ1ЃЉЙЫПЭГщНБ1ДЮФмЛёНБЕФЧщПігаЃКЙЫПЭГщНБ1ДЮЛёвЛЕШНБЃЌЙЫПЭГщНБ1ДЮЛёЖўЕШНБЃЌЗжБ№ЧѓГіСНжжЧщПіЕФИХТЪВЂЯрМгМДЮЊЫљЧѓЃЛЃЈ2ЃЉЙЫПЭГщНБ3ДЮЮЊЖРСЂжиИДЪдбщЃЌгЩЃЈ1ЃЉжЊЃЌЙЫПЭГщНБ1ДЮЛёвЛЕШНБЕФИХТЪЮЊ![]() ЃЌИљОнnДЮЖРСЂжиИДЪЕбщжаЧЁКУЗЂЩњkДЮЕФИХТЪЙЋЪНPЃЈX=kЃЉ=
ЃЌИљОнnДЮЖРСЂжиИДЪЕбщжаЧЁКУЗЂЩњkДЮЕФИХТЪЙЋЪНPЃЈX=kЃЉ=![]() pk(1-pЃЉn-kЗжБ№ЧѓГіXЫљгаПЩФмШЁжЕЕФИХТЪЃЌСаГіЗжВМСаЃЌИљОнЗўДгЖўЯюЗжВМЕФРыЩЂаЭЫцЛњБфСПЕФЪ§бЇЦкЭћEЃЈXЃЉ=npМДПЩЧѓНт.
pk(1-pЃЉn-kЗжБ№ЧѓГіXЫљгаПЩФмШЁжЕЕФИХТЪЃЌСаГіЗжВМСаЃЌИљОнЗўДгЖўЯюЗжВМЕФРыЩЂаЭЫцЛњБфСПЕФЪ§бЇЦкЭћEЃЈXЃЉ=npМДПЩЧѓНт.
ЁОПМЕуОЋЮіЁПБОЬтжївЊПМВщСЫРыЩЂаЭЫцЛњБфСПМАЦфЗжВМСаЕФЯрЙижЊЪЖЕуЃЌашвЊеЦЮедкЩфЛїЁЂВњЦЗМьбщЕШР§згжаЃЌЖдгкЫцЛњБфСПXПЩФмШЁЕФжЕЃЌЮвУЧПЩвдАДвЛЖЈДЮађвЛвЛСаГіЃЌетбљЕФЫцЛњБфСПНазіРыЩЂаЭЫцЛњБфСПЃЎРыЩЂаЭЫцЛњБфСПЕФЗжВМСаЃКвЛАуЕФ,ЩшРыЩЂаЭЫцЛњБфСПXПЩФмШЁЕФжЕЮЊx1,x2,.....,xi,......,xnЃЌXШЁУПвЛИіжЕ xi(i=1,2,......ЃЉЕФИХТЪP(ІЮ=xiЃЉЃНPiЃЌдђГЦБэЮЊРыЩЂаЭЫцЛњБфСПX ЕФИХТЪЗжВМЃЌМђГЦЗжВМСаВХФме§ШЗНтД№ДЫЬтЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєжБЯпl1ЃКy=x+aКЭl2ЃКy=x+bНЋдВЃЈxЉ1ЃЉ2+ЃЈyЉ2ЃЉ2=8ЗжГЩГЄЖШЯрЭЌЕФЫФЖЮЛЁЃЌдђab= ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊжБЯпЯЕЗНГЬ![]() ЃЈЦфжа
ЃЈЦфжа![]() ЮЊВЮЪ§ЃЉЃЎЕБ
ЮЊВЮЪ§ЃЉЃЎЕБ![]() ЪБЃЌжБЯп
ЪБЃЌжБЯп![]() гыСНзјБъжсЫљЮЇГЩЕФШ§НЧаЮЕФУцЛ§ЮЊ__________ЃЌШєИУжБЯпЯЕжаЕФШ§ЬѕжБЯпЮЇГЩе§Ш§НЧаЮЧјгђ
гыСНзјБъжсЫљЮЇГЩЕФШ§НЧаЮЕФУцЛ§ЮЊ__________ЃЌШєИУжБЯпЯЕжаЕФШ§ЬѕжБЯпЮЇГЩе§Ш§НЧаЮЧјгђ![]() ЃЌдђЧјгђ
ЃЌдђЧјгђ![]() ЕФУцЛ§ЮЊ__________ЃЎ
ЕФУцЛ§ЮЊ__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбЁао4Љ1ЃКМИКЮжЄУїбЁНВ
ШчЭМЃЌЁбOКЭЁбOЁфЯрНЛгкAЃЌBСНЕуЃЌЙ§AзїСНдВЕФЧаЯпЗжБ№НЛСНдВгкCЁЂDСНЕуЃЌСЌНгDBВЂбгГЄНЛЁбOгкЕуEЃЎжЄУїЃК
ЃЈ1ЃЉACBD=ADABЃЛ
ЃЈ2ЃЉAC=AEЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПДг5УћХЎЭЌбЇКЭ4УћФаЭЌбЇжабЁГі4ШЫВЮМгЫФГЁВЛЭЌЕФбнНВЃЌЗжБ№АДЯТСавЊЧѓЃЌИїгаЖрЩйжжВЛЭЌбЁЗЈЃПЃЈгУЪ§зжзїД№ЃЉ
ЃЈ1ЃЉФаЁЂХЎЭЌбЇИї2УћЃЛ
ЃЈ2ЃЉФаЁЂХЎЭЌбЇЗжБ№жСЩйга1УћЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЧАЬсЯТЃЌФаЭЌбЇМзгыХЎЭЌбЇввВЛФмЭЌЪБбЁГіЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§f(x)ЃНx2ЃЋaxЃЋb ЃЌ g(x)ЃНex(cxЃЋd)ЃЌШєЧњЯпyЃНf(x)КЭЧњЯпyЃНg(x)ЖМЙ§ЕуP(0ЃЌ2)ЃЌЧвдкЕуPДІгаЯрЭЌЕФЧаЯпyЃН4xЃЋ2ЃЎ
ЃЈ1ЃЉЧѓa ЃЌ b ЃЌ c ЃЌ dЕФжЕЃЛ
ЃЈ2ЃЉШєxЁнЃ2ЪБЃЌКугаf(x)Ёмkg(x)ЃЌЧѓkЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌвбжЊA(5ЃЌЃ2)ЃЌB(7,3)ЃЌЧвACБпЕФжаЕуMдкyжсЩЯЃЌBCЕФжаЕуNдкxжсЩЯЃЎ

(1)ЧѓЕуCЕФзјБъЃЛ
(2)Чѓ![]() БпЩЯЕФжаЯпЫљдкжБЯпЗНГЬЃЎ
БпЩЯЕФжаЯпЫљдкжБЯпЗНГЬЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПКЏЪ§fЃЈxЃЉЃНxlnxЃaЃЈxЃ1ЃЉ2ЃxЃЌgЃЈxЃЉЃНlnxЃ2aЃЈxЃ1ЃЉЃЌЦфжаГЃЪ§aЁЪRЃЎ
ЃЈЂёЃЉЬжТлgЃЈxЃЉЕФЕЅЕїадЃЛ
ЃЈЂђЃЉЕБaЃО0ЪБЃЌШєfЃЈxЃЉгаСНИіСуЕуx1 ЃЌ x2ЃЈx1ЃМx2ЃЉЃЌЧѓжЄЃКдкЧјМфЃЈ1ЃЌЃЋЁоЃЉЩЯДцдкfЃЈxЃЉЕФМЋжЕЕуx0 ЃЌ ЪЙЕУx0lnx0ЃЋlnx0Ѓ2x0ЃО0ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЪ§Са![]() ЕФЧАnЯюКЭ
ЕФЧАnЯюКЭ![]() .ЧѓЃК
.ЧѓЃК
ЃЈIЃЉЧѓЪ§Са![]() ЕФЭЈЯюЙЋЪНЃЛ
ЕФЭЈЯюЙЋЪНЃЛ
ЃЈIIЃЉЧѓЪ§Са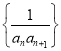 ЕФЧАnЯюКЭ
ЕФЧАnЯюКЭ![]() ЃЛ
ЃЛ
ЃЈIIIЃЉЧѓ![]() ЕФзюаЁжЕ.
ЕФзюаЁжЕ.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com