
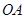 ,
, 是某地一个湖泊的两条互相垂直的湖堤,线段
是某地一个湖泊的两条互相垂直的湖堤,线段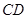 和曲线段
和曲线段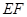 分别是湖泊中的一座栈桥和一条防波堤.为观光旅游的需要,拟过栈桥
分别是湖泊中的一座栈桥和一条防波堤.为观光旅游的需要,拟过栈桥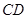 上某点
上某点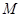 分别修建与
分别修建与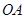 ,
, 平行的栈桥
平行的栈桥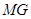 、
、 ,且以
,且以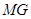 、
、 为边建一个跨越水面的三角形观光平台
为边建一个跨越水面的三角形观光平台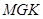 .建立如图2所示的直角坐标系,测得线段
.建立如图2所示的直角坐标系,测得线段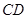 的方程是
的方程是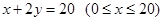 ,曲线段
,曲线段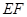 的方程是
的方程是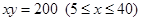 ,设点
,设点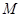 的坐标为
的坐标为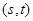 ,记
,记 .(题中所涉及的长度单位均为米,栈桥和防波堤都不计宽度)
.(题中所涉及的长度单位均为米,栈桥和防波堤都不计宽度)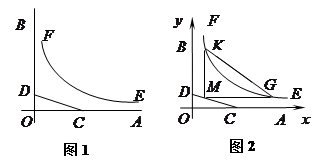
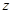 的取值范围;
的取值范围;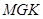 面积
面积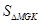 关于
关于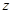 的函数解析式,并求出该面积的最小值
的函数解析式,并求出该面积的最小值科目:高中数学 来源:不详 题型:解答题
 表示神风摩托车厂一天的销售收入与摩托车销售量的关系;
表示神风摩托车厂一天的销售收入与摩托车销售量的关系; 表示摩托车厂一天的销售成本与销售量的关系.
表示摩托车厂一天的销售成本与销售量的关系.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
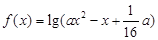 的定义域为R;命题q:不等式
的定义域为R;命题q:不等式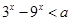 对任意
对任意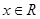 恒成立.
恒成立.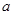 的取值范围;
的取值范围;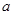 的取值范围.
的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com