
【题目】已知圆![]() 经过点A(-2,0),B(0,2),且圆心
经过点A(-2,0),B(0,2),且圆心![]() 在直线y=x上,又直线l:y=kx+1与圆
在直线y=x上,又直线l:y=kx+1与圆![]() 相交于P、Q两点.
相交于P、Q两点.
(1)求圆![]() 的方程;
的方程;
(2)若![]() ,求实数k的值;
,求实数k的值;
(3)过点![]() 作动直线
作动直线![]() 交圆
交圆![]() 于
于![]() ,
,![]() 两点.试问:在以
两点.试问:在以![]() 为直径的所有圆中,是否存在这样的圆
为直径的所有圆中,是否存在这样的圆![]() ,使得圆
,使得圆![]() 经过点
经过点![]() ?若存在,求出圆
?若存在,求出圆![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在圆
;(3)存在圆![]() 或
或![]() ,使得圆
,使得圆![]() 经过点
经过点![]() .
.
【解析】
试题分析:(1)根据题意设出圆心![]() 和半径
和半径![]() ,列出
,列出![]() 和
和![]() 的方程,求得圆的方程;(2)根据
的方程,求得圆的方程;(2)根据![]() ,
,
求得![]() ,所以圆心到直线
,所以圆心到直线![]() 的距离为
的距离为![]() ,求得
,求得![]() 的值;(3)若圆
的值;(3)若圆![]() 经过点
经过点![]() ,则必有
,则必有![]() 即
即![]() ①,当直线
①,当直线![]() 的斜率不存在时,显然满足题意得圆,当直线
的斜率不存在时,显然满足题意得圆,当直线![]() 的斜率存在时,设其斜率为
的斜率存在时,设其斜率为![]() ,直线
,直线![]() 的方程为:
的方程为:![]() ,代入圆
,代入圆![]() 的方程,由韦达定理,得到
的方程,由韦达定理,得到![]() 的值,联立①解得
的值,联立①解得![]() 的值,存在所求的圆,进而得到所求的圆的方程.
的值,存在所求的圆,进而得到所求的圆的方程.
试题解析:(1)设圆心C(a,a),半径为r.因为圆C经过点A(-2,0),B(0,2),所以|AC|=|BC|=r,易得a=0,r=2,所以圆C的方程是![]() . 3分
. 3分
(2)因为![]() ·
·![]() =2×2×cos〈
=2×2×cos〈![]() ,
,![]() 〉=-2,且
〉=-2,且![]() 与
与![]() 的夹角为∠POQ,
的夹角为∠POQ,
所以cos∠POQ=-![]() ,∠POQ=120°,所以圆心C到直线l:kx-y+1=0的距离d=1,
,∠POQ=120°,所以圆心C到直线l:kx-y+1=0的距离d=1,
又d=![]() ,所以
,所以![]() . 7分
. 7分
(联立直线与圆的方程求解酌情给分)
(3)(ⅰ)当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 经过圆
经过圆![]() 的圆心
的圆心![]() ,此时直线
,此时直线![]() 与圆
与圆![]() 的交点为
的交点为![]() ,
,![]() ,
,![]() 即为圆
即为圆![]() 的直径,而点
的直径,而点![]() 在圆
在圆![]() 上,即圆
上,即圆![]() 也是满足题意的圆 8分
也是满足题意的圆 8分
(ⅱ)当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() ,由
,由![]() ,
,
消去![]() 整理,得
整理,得![]() ,由△
,由△![]() ,得
,得![]() 或
或![]() .
.
设![]() ,则有
,则有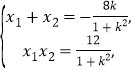 ① 9分
① 9分
由①得![]() , ②
, ②
![]() , ③
, ③
若存在以![]() 为直径的圆
为直径的圆![]() 经过点
经过点![]() ,则
,则![]() ,所以
,所以![]() ,
,
因此![]() ,即
,即![]() , 10分
, 10分
则![]() ,所以
,所以![]() ,
,![]() ,满足题意. 12分
,满足题意. 12分
此时以![]() 为直径的圆的方程为
为直径的圆的方程为![]() ,
,
即![]() ,亦即
,亦即![]() . 13分
. 13分
综上,在以![]() 为直径的所有圆中,存在圆
为直径的所有圆中,存在圆![]() :
:![]() 或
或
![]() ,使得圆
,使得圆![]() 经过点
经过点![]() . 14分
. 14分


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:
【题目】为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,下表记录了小李某月1号到5号每天打篮球时间x(单位:小时)与当天投篮命中率y之间的关系:
时间x | 1 | 2 | 3 | 4 | 5 |
命中率y | 0.4 | 0.5 | 0.6 | 0.6 | 0.4 |
小李这5天的平均投篮命中率为 ;用线性回归分析的方法,预测小李该月6号打6小时篮球的投篮命中率为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,椭圆C和抛物线y2=x交于M,N两点,且直线MN恰好通过椭圆C的右焦点.
,椭圆C和抛物线y2=x交于M,N两点,且直线MN恰好通过椭圆C的右焦点.
(1)求椭圆C的标准方程;
(2)经过椭圆C右焦点的直线l和椭圆C交于A,B两点,点P在椭圆上,且 ![]() =2
=2 ![]() ,其中O为坐标原点,求直线l的斜率.
,其中O为坐标原点,求直线l的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一盒中装有9张各写有一个数字的卡片,其中4张卡片上的数字是1,3张卡片上的数字是2,2张卡片上的数字是3,从盒中任取3张卡片.
(1)求所取3张卡片上的数字完全相同的概率;
(2)X表示所取3张卡片上的数字的中位数,求X的分布列与数学期望.(注:若三个数字a,b,c满足a≤b≤c,则称b为这三个数的中位数.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设圆(x+1)2+y2=25的圆心为C,A(1,0)是圆内一定点,Q为圆周上任一点.线段AQ的垂直平分线与CQ的连线交于点M,则M的轨迹方程为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx,x1 , x2∈(0, ![]() ),且x1<x2 , 则下列结论中正确的是( )
),且x1<x2 , 则下列结论中正确的是( )
A.(x1﹣x2)[f(x1)﹣f(x2)]<0
B.f( ![]() )<f(
)<f( ![]() )
)
C.x1f(x2)>x2f(x1)
D.x2f(x2)>x1f(x1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中, 平面
中, 平面![]() 平面
平面![]() ,
,![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在, 求
?若存在, 求![]() 的值;若不存在, 说明理由.
的值;若不存在, 说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在
是定义在![]() 上的偶函数,且当
上的偶函数,且当![]() 时,
时,![]() .
.

(1)已画出函数![]() 在
在![]() 轴左侧的图像,如图所示,请补出完整函数
轴左侧的图像,如图所示,请补出完整函数![]() 的图像,并根据图像写出函数
的图像,并根据图像写出函数![]() 的增区间;
的增区间;
⑵写出函数![]() 的解析式和值域.
的解析式和值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com