
【题目】已知![]() ,函数
,函数![]() .
.
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程.
处的切线方程.
(Ⅱ)求![]() 在区间
在区间![]() 上的最小值.
上的最小值.
【答案】(![]() )
)![]() .(
.(![]() )见解析.
)见解析.
【解析】试题分析:(1)求出f'(x),得切线的斜率![]() ,又曲线的切点为(2,f(2)),由点斜式可写出切线方程;
,又曲线的切点为(2,f(2)),由点斜式可写出切线方程;
(2)借助于导数,将函数![]() 的最值问题转化为导函数进行研究.分
的最值问题转化为导函数进行研究.分![]() ,
, ![]() ,
, ![]() 三种情况讨论函数的最值情况.
三种情况讨论函数的最值情况.
试题解析:(![]() )当
)当![]() 时,
时, ![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
,
∴![]() ,即曲线
,即曲线![]() 在点
在点![]() 处的切线斜率为
处的切线斜率为![]() .
.
又∵![]() ,
,
∴曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,
,
即![]() .
.
(![]() )∵
)∵![]() ,∴
,∴![]() .
.
令![]() ,得
,得![]() .
.
①若![]() ,则
,则![]() ,
, ![]() 在区间
在区间![]() 上单调递增,此时函数
上单调递增,此时函数![]() 无最小值.
无最小值.
②若![]() ,当
,当![]() 时,
时, ![]() ,函数
,函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,
当![]() 时,
时, ![]() ,函数
,函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
所以当![]() 时,函数
时,函数![]() 取得最小值
取得最小值![]() .
.
③当![]() ,则当
,则当![]() 时,
时, ![]() ,函数
,函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,
所以当![]() 时,函数
时,函数![]() 取得最小值
取得最小值![]() .
.
综上所述,当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上无最小值.
上无最小值.
当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() .
.
当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() .
.


科目:高中数学 来源: 题型:
【题目】要分析学生初中升学考试的数学成绩对高一年级数学学习有什么影响,在高一年级学生中随机抽取10名学生,分析他们入学的数学成绩(x)和高一年级期末数学考试成绩(y)(如下表):
(1)画出散点图;
(2)判断入学成绩(x)与高一期末考试成绩(y)是否有线性相关关系;
(3)如果x与y具有线性相关关系,求出回归直线方程;
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
x | 63 | 67 | 45 | 88 | 81 | 71 | 52 | 99 | 58 | 76 |
y | 65 | 78 | 52 | 85 | 92 | 89 | 73 | 98 | 56 | 75 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某花店每天以每枝![]() 元的价格从农场购进若干枝玫瑰花,然后以每枝
元的价格从农场购进若干枝玫瑰花,然后以每枝![]() 元的价格出售.如果当天卖不完,剩下的玫瑰花做垃圾处理.
元的价格出售.如果当天卖不完,剩下的玫瑰花做垃圾处理.
(1)若花店一天购进![]() 枝玫瑰花,求当天的利润
枝玫瑰花,求当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:枝,
(单位:枝, ![]() )的函数解析式.
)的函数解析式.
(2)花店记录了![]() 天玫瑰花的日需求量(单位:枝),整理得下表:
天玫瑰花的日需求量(单位:枝),整理得下表:
日需求量 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|
假设花店在这![]() 天内每天购进
天内每天购进![]() 枝玫瑰花,求这
枝玫瑰花,求这![]() 天的日利润(单位:元)的平均数.
天的日利润(单位:元)的平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以原点
),以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() 是曲线
是曲线![]() 上一点,若点
上一点,若点![]() 到曲线
到曲线![]() 的最小距离为
的最小距离为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年某市政府为了有效改善市区道路交通拥堵状况出台了一系列的改善措施,其中市区公交站点重新布局和建设作为重点项目.市政府相关部门根据交通拥堵情况制订了“市区公交站点重新布局方案”,现准备对该“方案”进行调查,并根据调查结果决定是否启用该“方案”.调查人员分别在市区的各公交站点随机抽取若干市民对该“方案”进行评分,并将结果绘制成如图所示的频率分布直方图.相关规则为:①调查对象为本市市民,被调查者各自独立评分;②采用百分制评分,[60,80)内认定为满意,不低于80分认定为非常满意;③市民对公交站点布局的满意率不低于75%即可启用该“方案”;④用样本的频率代替概率.
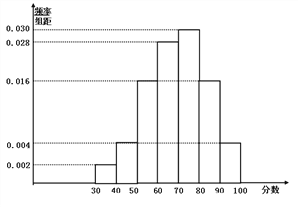
(1)从该市800万人的市民中随机抽取5人,求恰有2人非常满意该“方案”的概率;并根据所学统计学知识判断该市是否启用该“方案”,说明理由.
(2)已知在评分低于60分的被调查者中,老年人占![]() ,现从评分低于60分的被调查者中按年龄分层抽取9人以便了解不满意的原因,并从中抽取3人担任群众督查员,记
,现从评分低于60分的被调查者中按年龄分层抽取9人以便了解不满意的原因,并从中抽取3人担任群众督查员,记![]() 为群众督查员中的老人的人数,求随机变量
为群众督查员中的老人的人数,求随机变量![]() 的分布列及其数学期望
的分布列及其数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学名著《九章算术》中有这样一个问题:今有牛、马、羊食人苗,苗主责之粟五斗,羊主曰:“我羊食半马.”马主曰:“我马食半牛.”今欲衰偿之,问各出几何?此问题的译文是:今有牛、马、羊吃了别人的禾苗,禾苗主人要求赔偿5斗粟.羊主人说:“我羊所吃的禾苗只有马的一半.”马主人说:“我马所吃的禾苗只有牛的一半.”打算按此比例偿还,他们各应偿还多少?已知牛、马、羊的主人各应偿还![]() 升,
升, ![]() 升,
升, ![]() 升,1斗为10升,则下列判断正确的是( )
升,1斗为10升,则下列判断正确的是( )
A. ![]() ,
, ![]() ,
, ![]() 依次成公比为2的等比数列,且
依次成公比为2的等比数列,且![]()
B. ![]() ,
, ![]() ,
, ![]() 依次成公比为2的等比数列,且
依次成公比为2的等比数列,且![]()
C. ![]() ,
, ![]() ,
, ![]() 依次成公比为
依次成公比为![]() 的等比数列,且
的等比数列,且![]()
D. ![]() ,
, ![]() ,
, ![]() 依次成公比为
依次成公比为![]() 的等比数列,且
的等比数列,且![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标![]() 中,圆
中,圆![]() ,圆
,圆![]() 。
。
(Ⅰ)在以O为极点,x轴正半轴为极轴的极坐标系中,分别写出圆![]() 的极坐标方程,并求出圆
的极坐标方程,并求出圆![]() 的交点坐标(用极坐标表示);
的交点坐标(用极坐标表示);
(Ⅱ)求圆![]() 的公共弦的参数方程。
的公共弦的参数方程。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com