
【题目】如果![]() 不是等差数列,但若
不是等差数列,但若![]() ,使得
,使得![]() ,那么称
,那么称![]() 为“局部等差”数列.已知数列
为“局部等差”数列.已知数列![]() 的项数为4,记事件
的项数为4,记事件![]() :集合
:集合![]() ,事件
,事件![]() :
:![]() 为“局部等差”数列,则条件概率
为“局部等差”数列,则条件概率![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() 是函数
是函数![]() 的图象上任意两点,若
的图象上任意两点,若![]() 为
为![]() ,
,![]() 的中点,且
的中点,且![]() 的横坐标为
的横坐标为![]() .
.
(1)求![]() ;
;
(2)若![]() ,
,![]() ,求
,求![]() ;
;
(3)已知数列![]() 的通项公式
的通项公式![]() (
(![]() ,
,![]() ),数列
),数列![]() 的前
的前![]() 项和为
项和为![]() ,若不等式
,若不等式![]() 对任意
对任意![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前n项和为
的前n项和为![]() ,对任意的正整数n,都有
,对任意的正整数n,都有![]() 成立,记
成立,记![]() .
.
(1)求数列![]() 与数列
与数列![]() 的通项公式;
的通项公式;
(2)求证:①![]() 对
对![]() 恒成立.②
恒成立.②![]() 对
对![]() 恒成立,其中
恒成立,其中![]() 为数列
为数列![]() 的前n项和.
的前n项和.
(3)记![]() ,
,![]() 为
为![]() 的前n项和,求证:对任意正整数n,都有
的前n项和,求证:对任意正整数n,都有![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 经过点
经过点![]() .
.
(1)求抛物线![]() 的方程及其准线方程;
的方程及其准线方程;
(2)设![]() 为原点,过抛物线
为原点,过抛物线![]() 的焦点作斜率不为0的直线
的焦点作斜率不为0的直线![]() 交抛物线
交抛物线![]() 于两点
于两点![]() ,
,![]() ,直线
,直线![]() 分别交直线
分别交直线![]() ,
,![]() 于点
于点![]() 和点
和点![]() .求证:以
.求证:以![]() 为直径的圆经过
为直径的圆经过![]() 轴上的两个定点.
轴上的两个定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列说法:①方程![]() 表示的图形是一个点;②命题“若
表示的图形是一个点;②命题“若![]() ,则
,则![]() 或
或![]() ”为真命题;③已知双曲线
”为真命题;③已知双曲线![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,过右焦点
,过右焦点![]() 被双曲线截得的弦长为4的直线有3条;④已知椭圆
被双曲线截得的弦长为4的直线有3条;④已知椭圆![]() 上有两点
上有两点![]() ,
,![]() ,若点
,若点![]() 是椭圆
是椭圆![]() 上任意一点,且
上任意一点,且![]() ,直线
,直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,则
,则![]() 为定值
为定值![]() .
.
其中说法正确的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
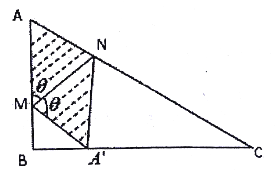
【题目】如图,某小区准备将闲置的一直角三角形地块开发成公共绿地,图中![]() .设计时要求绿地部分(如图中阴影部分所示)有公共绿地走道
.设计时要求绿地部分(如图中阴影部分所示)有公共绿地走道![]() ,且两边是两个关于走道
,且两边是两个关于走道![]() 对称的三角形(
对称的三角形(![]() 和
和![]() ).现考虑方便和绿地最大化原则,要求点
).现考虑方便和绿地最大化原则,要求点![]() 与点
与点![]() 均不重合,
均不重合,![]() 落在边
落在边![]() 上且不与端点
上且不与端点![]() 重合,设
重合,设![]() .
.
(1)若![]() ,求此时公共绿地的面积;
,求此时公共绿地的面积;
(2)为方便小区居民的行走,设计时要求![]() 的长度最短,求此时绿地公共走道
的长度最短,求此时绿地公共走道![]() 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学从甲、乙两个班中各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班学生成绩的众数是83,乙班学生成绩的平均数是86,则![]() 的值为( )
的值为( )
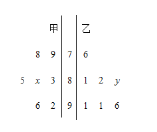
A.7B.8C.9D.10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com