解:
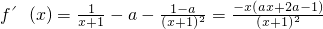
,x>-1,(2分)
(I)由题意可得
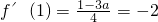
,解得a=3,(3分)
因为f(1)=ln2-4,此时在点(1,f(1))处的切线方程为y-(ln2-4)=-2(x-1),
即y=-2x+ln2-2,与直线l:y=-2x+1平行,故所求a的值为3.(4分)
(II)令f'(x)=0,得到
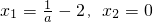
,
由

可知
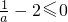
,即x
1≤0.(5分)
①即

时,
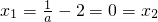
所以,
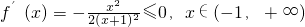
,(6分)
故f(x)的单调递减区间为(-1,+∞).(7分)
②当

时,
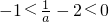
(6分),即-1<x
1<0=x
2,
所以,在区间
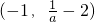
和(0,+∞)上,f′(x)<0;(8分)
在区间
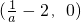
上,f′(x)>0.(9分)
故f(x)的单调递减区间是
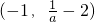
和(0,+∞),单调递增区间是
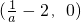
.(10分)
③当a≥1时,
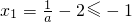
,
所以,在区间(-1,0)上f'(x)>0;(11分)
在区间(0,+∞)上f'(x)<0,(12分)
故f(x)的单调递增区间是(-1,0),单调递减区间是(0,+∞).(13分)
综上讨论可得:
当

时,函数f(x)的单调递减区间是(-1,+∞);
当

时,函数f(x)的单调递减区间是
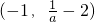
和(0,+∞),单调递增区间是
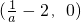
;
当a≥1时,函数f(x)的单调递增区间是(-1,0),单调递减区间是(0,+∞).
分析:(Ⅰ)由题设条件,求出函数的导数,由于曲线y=f(x)在(1,f(1))处的切线与直线l:y=-2x+1平行时,由导数的几何意义建立关于参数a的方程求出其值即可.
(Ⅱ)由函数的导数中存在参数a,它的取值范围对函数的单调性有影响,故要对其进行分类讨论,在确定的范围下求出函数的单调区间.
点评:本题考查利用导数研究曲线上某点处的切线方程,求解本题的重点是理解导数的几何意义以及分类讨论的思想方法,分类讨论的思想在高中数学中用途广泛,其特点是在解题中出现了不确定情况,由分类变不确定为确定.本题运算量较大,思维量也大,易因为马虎或者耐心不够而出错,造成解题失败,做题时要养成好习惯,要严谨,认真.

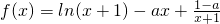 (
( ).
).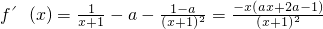 ,x>-1,(2分)
,x>-1,(2分)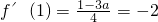 ,解得a=3,(3分)
,解得a=3,(3分)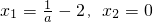 ,
, 可知
可知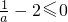 ,即x1≤0.(5分)
,即x1≤0.(5分) 时,
时,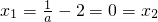
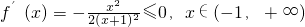 ,(6分)
,(6分) 时,
时,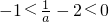 (6分),即-1<x1<0=x2,
(6分),即-1<x1<0=x2,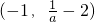 和(0,+∞)上,f′(x)<0;(8分)
和(0,+∞)上,f′(x)<0;(8分)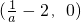 上,f′(x)>0.(9分)
上,f′(x)>0.(9分)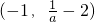 和(0,+∞),单调递增区间是
和(0,+∞),单调递增区间是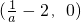 .(10分)
.(10分)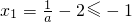 ,
, 时,函数f(x)的单调递减区间是(-1,+∞);
时,函数f(x)的单调递减区间是(-1,+∞); 时,函数f(x)的单调递减区间是
时,函数f(x)的单调递减区间是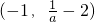 和(0,+∞),单调递增区间是
和(0,+∞),单调递增区间是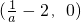 ;
;

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<