Question

【题目】如图，在海岛A上有一座海拔1千米的山，山顶设有一个观察站P，上午11时，测得一轮船在岛北偏东30°，俯角为30°的B处，到11时10分又测得该船在岛北偏西60°，俯角为60°的C处．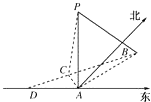
（1）求船的航行速度是每小时多少千米？
（2）又经过一段时间后，船到达海岛的正西方向的D处，问此时船距岛A有多远？

Answer 1

【答案】
（1）解：在Rt△PAB中，∠APB=60°，PA=1，∴AB= ．

在Rt△PAC中，∠APC=30°，

∴AC= ．

在△ACB中，∠CAB=30°+60°=90°，

∴BC= = = ．

则船的航行速度为 ÷ =2 （千米/时）

（2）解：在△ACD、中，∠DAC=90°﹣60°=30°，

sin∠DCA=sin（180°﹣∠ACB）=sin∠ACB= = = ，

sin∠CDA=sin（∠ACB﹣30°）

=sin∠ACBcos30°﹣cos∠ACBsin30°

= ﹣

= ．

由正弦定理得 = ．

∴AD= = = ．

故此时船距岛A有 千米

【解析】（1）先Rt△PAB、Rt△PAC中确定AB、AC的长，进而求得，∠CAB=30°+60°=90°，最后利用勾股定理求得BC，用里程除以时间即为船的速度．（2）利用sin∠DCA=sin（180°﹣∠ACB）=sin∠ACB求得sin∠DCA的值，利用sin∠CDA=sin（∠ACB﹣30°）=sin∠ACBcos30°﹣cos∠ACBsin30°求得sin∠CDA的值，进而利用正弦定理求得AD．