
【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)若关于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:
【题目】已知动点![]() 满足:
满足: ![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() (点
(点![]() 与点
与点![]() 不重合),证明:直线
不重合),证明:直线![]() 恒过定点,并求该定点的坐标.
恒过定点,并求该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,若![]() ,
,![]() ,且
,且![]() .
.
(Ⅰ)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)设(Ⅰ)中曲线![]() 的左、右顶点分别为
的左、右顶点分别为![]() 、
、![]() ,过点
,过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于两点
交于两点![]() ,
,![]() (不与
(不与![]() ,
,![]() 重合).若直线
重合).若直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,试判断点
,试判断点![]() ,
,![]() ,
,![]() 是否共线,并说明理由.
是否共线,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年7月1日,《上海市生活垃圾管理条例》正式实施,生活垃圾要按照“可回收物”、“有害垃圾”、“湿垃圾”、“干垃圾”的分类标准进行分类,没有垃圾分类和未投放到指定垃圾桶内等会被罚款和行政处罚.若某上海居民提着厨房里产生的“湿垃圾”随意地投放到楼下的垃圾桶,若楼下分别放有“可回收物”、“有害垃圾”、“湿垃圾”、“干垃圾”四个垃圾桶,则该居民会被罚款和行政处罚的概率为( )




A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网店经营各种儿童玩具,该网店老板发现该店经销的一种手腕可以摇动的![]() 款芭比娃娃玩具在某周内所获纯利
款芭比娃娃玩具在某周内所获纯利![]() (元)与该周每天销售这种芭比娃娃的个数
(元)与该周每天销售这种芭比娃娃的个数![]() (个)之间的关系如下表:
(个)之间的关系如下表:
每天销售芭比娃娃个数 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
该周内所获纯利 | 66 | 69 | 74 | 81 | 89 | 90 | 91 |
(1)由表中数据可推测![]() 线性相关,求出回归直线方程;
线性相关,求出回归直线方程;
(2)请你预测当该店每天销售这种芭比娃娃20件时,每周获纯利多少?
参考公式: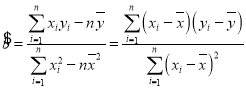 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 垂直圆O所在的平面,
垂直圆O所在的平面,![]() 是圆O的一条直径,C为圆周上异于A,B的动点,D为弦
是圆O的一条直径,C为圆周上异于A,B的动点,D为弦![]() 的中点,
的中点,![]() .
.
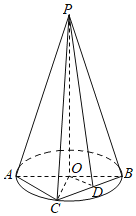
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是函数y=f(x)的导函数,定义
是函数y=f(x)的导函数,定义![]() 为
为![]() 的导函数,若方程
的导函数,若方程![]() =0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的拐点,经研究发现,所有的三次函数f(x)=ax3+bx2+cx+d(a≠0)都有拐点,且都有对称中心,其拐点就是对称中心,设f(x)=x3﹣3x2﹣3x+6,则f(
=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的拐点,经研究发现,所有的三次函数f(x)=ax3+bx2+cx+d(a≠0)都有拐点,且都有对称中心,其拐点就是对称中心,设f(x)=x3﹣3x2﹣3x+6,则f(![]() )+f(
)+f(![]() )+……+f(
)+……+f(![]() )=_____.
)=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com