
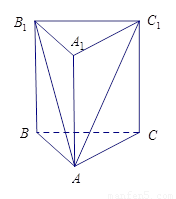
如图,已知正三棱柱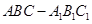 中,
中,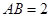 ,
,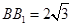 ,
,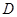 为
为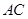 上的动点.
上的动点.
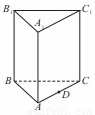
(1)求五面体 的体积;
的体积;
(2)当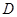 在何处时,
在何处时,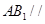 平面
平面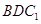 ,请说明理由;
,请说明理由;
(3)当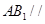 平面
平面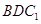 时,求证:平面
时,求证:平面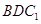
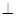 平面
平面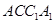 .
.
(1)4;(2)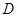 为
为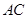 的中点;(3)证明过程详见解析.
的中点;(3)证明过程详见解析.
【解析】
试题分析:本题主要以正三棱柱为几何背景,考查椎体体积、线面平行、面面垂直的判定,运用传统几何法求解证明,突出考查空间想象能力和计算能力.第一问,由图形判断五面体就是四棱锥,所以主要任务就是求高和底面面积;第二问,利用直线与平面平行的性质定理,证明出 ,所以
,所以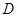 为
为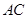 中点;第三问,结合第二问的结论,由线面垂直的判定定理,得出
中点;第三问,结合第二问的结论,由线面垂直的判定定理,得出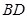 ⊥平面
⊥平面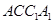 ,再由面面垂直的判定定理得出结果.
,再由面面垂直的判定定理得出结果.
试题解析:(Ⅰ)如图可知五面体是四棱锥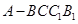 ,
,
∵侧面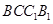 垂直于底面
垂直于底面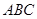 ,
,
∴正三角形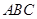 的高
的高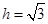 就是这个四棱锥
就是这个四棱锥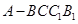 的高,
的高,
又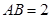 ,
,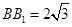 .
.
于是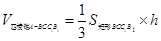
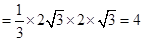 . 4分
. 4分
(Ⅱ)当点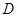 为
为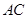 中点时,
中点时,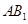 ∥平面
∥平面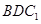 .
.
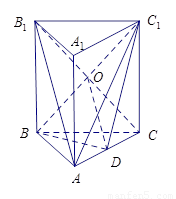
连结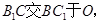 连结
连结 ,∵四边形
,∵四边形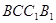 是矩形,
是矩形,
∴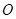 为
为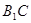 中点,
中点,
∵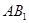 ∥平面
∥平面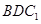 ,平面
,平面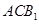
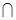 平面
平面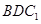 =
= ,
,
∴ ,∴
,∴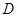 为
为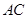 的中点.
8分
的中点.
8分
(Ⅲ)由(Ⅱ)可知当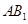 ∥平面
∥平面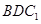 时,
时,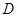 为
为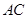 的中点.
的中点.
∵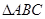 为正三角形,
为正三角形,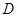 为
为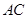 的中点,∴
的中点,∴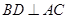 ,
,
由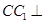 平面
平面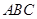 ,∴
,∴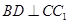 ,
,
又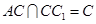 ,∴
,∴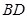 ⊥平面
⊥平面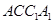 ,
,
又 平面
平面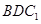 ,∴平面
,∴平面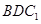 ⊥平面
⊥平面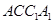 .
12分
.
12分
考点:1.直线与平面平行的性质定理;2.线面垂直的判定定理;3.面面垂直的判定定理.


 优生乐园系列答案
优生乐园系列答案科目:高中数学 来源: 题型:
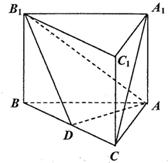 (2011•盐城模拟)如图,已知正三棱柱ABC-A1B1C1中,D是BC的中点.
(2011•盐城模拟)如图,已知正三棱柱ABC-A1B1C1中,D是BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
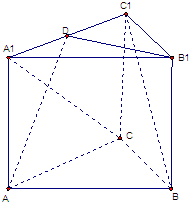 (2008•南京二模)如图,已知正三棱柱ABC-A1B1C1中,AB=
(2008•南京二模)如图,已知正三棱柱ABC-A1B1C1中,AB=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
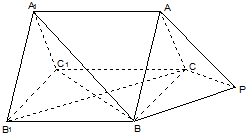 如图,已知正三棱柱ABC-A1B1C1中,AB=2
如图,已知正三棱柱ABC-A1B1C1中,AB=2| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知正三棱柱ABC-A1B1C1中,AB=2,BB1=2
如图,已知正三棱柱ABC-A1B1C1中,AB=2,BB1=2| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com