试题分析:
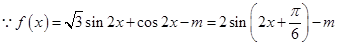
,由于
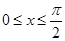
,故
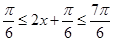
,
由于函数
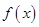
在区间
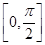
上有两个零点,所以
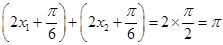
,所以
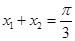
,
所以
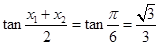
,故选D.
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
如图,已知点
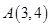
,
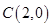
,点
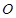
为坐标原点,点
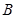
在第二象限,且
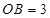
,记
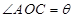
.

(1)求
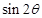
的值;(2)若
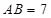
,求
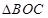
的面积.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知向量
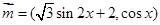
,
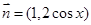
,设函数
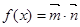
,
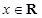
.
(Ⅰ)求
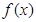
的最小正周期与最大值;
(Ⅱ)在
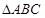
中,
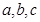
分别是角
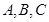
的对边,若
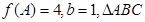
的面积为
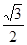
,求
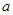
的值.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数

.
(1)若函数

的图像关于直线

对称,求

的最小值;
(2)若存在

,使

成立,求实数

的取值范围.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知向量

和

,
(1)设

,写出函数

的最小正周期;并求函数

的单调区间;
(2)若
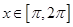
,求

的最大值.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知向量


,函数

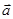
·

,且最小正周期为

.
(1)求

的值;
(2)设


,求

的值.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数

,

.
(Ⅰ)求函数

的最小值和最小正周期;
(Ⅱ)设

的内角

、

、

的对边分别为

、

、

,满足

,
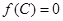
且

,求

、

的值.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知角

的始边与

轴的非负半轴重合,终边过点

,则

可以是( )
查看答案和解析>>
