
| 1 |
| 2 |
| X | 0 | 1 | 2 | 3 | ||||
| P |
|
m | n |
|
| 7 |
| 18 |
| 7 |
| 18 |
| 7 |
| 18 |
| 7 |
| 18 |
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:填空题
| 1 |
| 2 |
| X | 0 | 1 | 2 | 3 | ||||
| P |
|
m | n |
|
查看答案和解析>>
科目:高中数学 来源:2011-2012学年北京五中高二(上)期末数学试卷(理科)(解析版) 题型:填空题
 ,语文、英语取得优秀的概率分别为p,q(p>q),三科是否取得优秀是相互独立的,设随机变量X表示取得优秀的科目数,X的分布列如下
,语文、英语取得优秀的概率分别为p,q(p>q),三科是否取得优秀是相互独立的,设随机变量X表示取得优秀的科目数,X的分布列如下| X | 1 | 2 | 3 | |
| P |  | m | n |  |
查看答案和解析>>
科目:高中数学 来源:山西省康杰中学2010届高三5月模拟(理) 题型:解答题
某公司计划通过考试招聘一些员工,考试课目有语文、数学、物理、化学、已知某人能通过语文、数学、物理、化学考试的概率分别是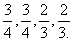 .现有两种方案
.现有两种方案
方案一:从语文、数学、物理、化学四门中随机抽取3门进行考试,3门都通过时才能录用.
方案二:四门都进行考试,其中有3门或3门以上通过时才能录用.
.1.求某人方案1被录用的概率;
.2.若用方案1进行之后,再用方案2再进行录取一些人,某人在参加方案1后,若录用,则不再考试,若没有录用,他一定也要参加方案2的考试,希望能被录用.某人参加考试的次数为 ,求
,求 的分布列和期望.
的分布列和期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com