
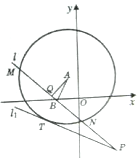
 已知以A(-1,2)点为圆心的圆与直线${l_1}:\frac{1}{2}x+y+\frac{7}{2}=0$相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点,直线l与l1相交于点P.
已知以A(-1,2)点为圆心的圆与直线${l_1}:\frac{1}{2}x+y+\frac{7}{2}=0$相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点,直线l与l1相交于点P.分析 (1)圆与直线${l_1}:\frac{1}{2}x+y+\frac{7}{2}=0$相切,利用圆心到直线的距离等于半径,可得r,可得圆A的方程;
(2)设出直线l的方程,y=k(x+2),Q是MN的中点,当$|{MN}|=2\sqrt{19}$时,QM=$\sqrt{19}$,利用圆心到直线的距离AQ,勾股定理可得K的值,可得直线l的方程.
(3)由直线l过B(-2,0),可分直线斜率存在和不存在两种进行讨论,分别讨论$\overrightarrow{BP}•\overrightarrow{BQ}$是否是定值.
解答 解:(1)设圆A的半径为r,圆与直线${l_1}:\frac{1}{2}x+y+\frac{7}{2}=0$相切,可得r=d=$\frac{|-1+4+7|}{\sqrt{5}}=2\sqrt{5}$
∴圆A的方程为(x+1)2+(y-2)2=20.
(2)当斜率k不存在时,即直线与x轴垂直,可得x=-2,符合题意;
当当斜率k存在时,设出直线l的方程,y=k(x+2),Q是MN的中点,当$|{MN}|=2\sqrt{19}$时,QM=$\sqrt{19}$.
AQ=$\sqrt{20-19}=1$,即圆心到直线y=k(x+2)的距离为1.
可得:$\frac{|k-2|}{\sqrt{{k}^{2}+1}}=1$,解得k=$\frac{3}{4}$
∴直线l的方程为x=-2或y=$\frac{3}{4}$(x+2).
(3)∵AQ⊥BP,
∴$\overrightarrow{BP}•\overrightarrow{BQ}$=($\overrightarrow{BA}+\overrightarrow{AQ}$)•$\overrightarrow{BP}$=$\overrightarrow{BA}•\overrightarrow{BP}+\overrightarrow{AQ}•\overrightarrow{BP}=\overrightarrow{BA}•\overrightarrow{BP}$.
①当斜率k不存在时,即直线与x轴垂直,可得P(-2,-$\frac{5}{2}$),$\overrightarrow{BP}=(0,-\frac{5}{2})$,又$\overrightarrow{BA}=(1,2)$,
∴$\overrightarrow{BQ}•\overrightarrow{BP}=\overrightarrow{BA}•\overrightarrow{BP}=-5$.
②当斜率k存在时,设直线l的方程,
由$\left\{\begin{array}{l}{y=k(x+2)}\\{x+2y+7=0}\end{array}\right.$解得P($\frac{-4k-7}{1+2k}$,$\frac{-5k}{1+2k}$),则$\overrightarrow{BP}=(\frac{-5}{1+2k},\frac{-5k}{1+2k})$,
∴$\overrightarrow{BQ}•\overrightarrow{BP}=\overrightarrow{BA}•\overrightarrow{BP}=\frac{-5}{1+2k}+\frac{-10k}{1+2k}$=-5
综上所得,$\overrightarrow{BP}•\overrightarrow{BQ}$是定值,且这个定值$\overrightarrow{BQ}•\overrightarrow{BP}=-5$.
点评 本题主要考查了直线与圆的方程的应用,直线的一般方程,圆的标准方程,弦长问题,点到直线的距离公式,斜率的存在性的讨论等,综合性强,计算量大.属于中档偏难.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | i<6 | B. | i<7 | C. | i<8 | D. | i<9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-∞,-\frac{3}{2}})$ | B. | $({-∞,-\frac{3}{4}})$ | C. | $({-\frac{3}{4},+∞})$ | D. | $({-\frac{3}{2},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1)n-1$\frac{1}{{3}^{n}}$ | B. | (-1)n-1$\frac{1}{3n}$ | C. | (-1)n$\frac{1}{{3}^{n}}$ | D. | (-1)n$\frac{1}{3n}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com