
在如图所示的多面体中,已知正三棱柱ABCA1B1C1的所有棱长均为2,四边形ABDC是菱形.
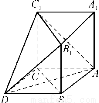
(1)求证:平面ADC1⊥平面BCC1B1;
(2)求该多面体的体积.
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第6课时练习卷(解析版) 题型:填空题
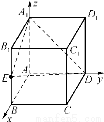
在正方体ABCDA1B1C1D1中,点E为BB1的中点,则平面A1ED与平面ABCD所成的锐二面角的余弦值为________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第5课时练习卷(解析版) 题型:解答题
在△ABC中,∠BAC=90°,∠B=60°,AB=1,D为线段BC的中点,E、F为线段AC的三等分点(如图①).将△ABD沿着AD折起到△AB′D的位置,连结B′C(如图②).
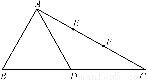
图①

图②
(1)若平面AB′D⊥平面ADC,求三棱锥B′-ADC的体积;
(2)记线段B′C的中点为H,平面B′ED与平面HFD的交线为l,求证:HF∥l;
(3)求证:AD⊥B′E.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第5课时练习卷(解析版) 题型:填空题
若等腰直角三角形的直角边长为2,则以一直角边所在的直线为轴旋转一周所成的几何体体积是__________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第4课时练习卷(解析版) 题型:解答题
如图,在多面体ABCDEF中,四边形ABCD是正方形,AB=2EF=2,EF∥AB,EF⊥FB,∠BFC=90°,BF=FC,G、H分别为DC、BC的中点.
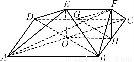
(1)求证:平面FGH∥平面BDE;
(2)求证:平面ACF⊥平面BDE.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第4课时练习卷(解析版) 题型:解答题
如图,在三棱锥SABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB,过A作AF⊥SB,垂足为F,点E、G分别是棱SA、
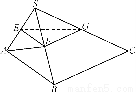
SC的中点.求证:
(1)平面EFG∥平面ABC;
(2)BC⊥SA.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第3课时练习卷(解析版) 题型:解答题
已知如图①所示,矩形纸片AA′A1′A1,点B、C、B1、C1分别为AA′、A1A1′的三等分点,将矩形纸片沿BB1、CC1折成如图②形状(正三棱柱),若面对角线AB1⊥BC1,求证:A1C⊥AB1.
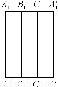
(图①)
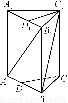
(图②)
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第1课时练习卷(解析版) 题型:填空题
已知点P、Q,平面α,将命题“P∈α,Q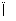 α
α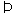 PQ
PQ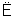 α”改成文字叙述是________.
α”改成文字叙述是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com