
【题目】函数![]()
(1)求![]() 的值;
的值;
(2)![]() 时,求
时,求![]() 的取值范围;
的取值范围;
(3)函数的性质通常指的是函数的定义域、值域、单调性、周期性、奇偶性等,请你探究函数![]() 其中的三个性质(直接写出结论即可)
其中的三个性质(直接写出结论即可)
【答案】(1)![]() (2)
(2)![]() (3)①定义域
(3)①定义域![]() ②值域
②值域![]() ③偶函数④
③偶函数④![]() ⑤在
⑤在![]()
![]() 单调递增,在
单调递增,在![]() 单调递减(写出任意三个即可)
单调递减(写出任意三个即可)
【解析】
(1)把所给的自变量的值代入函数式,根据诱导公式化简整理出结果.
(2)对函数式进行整理,得到y=Asin(ωx+φ)的形式,根据所给的角的范围写出ωx+φ的范围,根据三角函数的图象得到函数的值域.
(3)根据上一问整理出的函数的解析式,得到函数的定义域、值域、周期性、奇偶性、单调性等.
(1)![]() .
.
(2)当![]() 时,
时,![]() ,则sin2x≥0,cos2x≥0.
,则sin2x≥0,cos2x≥0.
∴![]()
又∵![]()
∴![]() ∴
∴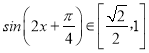
∴当![]() 时,f(x)的取值范围为
时,f(x)的取值范围为![]() .
.
(3)①f(x)的定义域为R;
②∵f(﹣x)=|sin(﹣2x)|+|cos(﹣2x)|=|sin2x|+|cos2x|=f(x)∴f(x)为偶函数.
③∵![]() ,
,
∴f(x)是周期为![]() 的周期函数;
的周期函数;
④由(2)可知,当![]() 时,
时,![]() ,
,
∴值域为![]() .
.
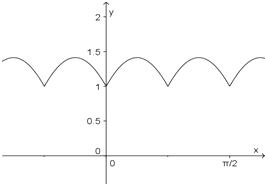
⑤可作出f(x)图象,如图所示:
由图象可知f(x)的增区间为![]() (k∈Z),
(k∈Z),
减区间为![]() (k∈Z) (写出任意三个即可)
(k∈Z) (写出任意三个即可)


科目:高中数学 来源: 题型:
【题目】某高校在2016年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下表所示.
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 | 0.050 |
第2组 |
| n | 0.350 |
第3组 |
| 30 | p |
第4组 |
| 20 | 0.200 |
第5组 |
| 10 | 0.100 |
合计 | 100 | 1.000 |
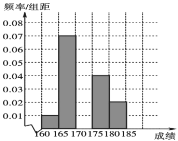
(1)求频率分布表中n,p的值,并估计该组数据的中位数(保留l位小数);
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样的方法抽取6名学生进入第二轮面试,则第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定从6名学生中随机抽取2名学生接受甲考官的面试,求第4组至少有1名学生被甲考官面试的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() 且满足:
且满足:![]()
(1)证明:![]() 是等比数列,并求数列
是等比数列,并求数列![]() 的通项公式.
的通项公式.
(2)设![]() ,若数列
,若数列![]() 是等差数列,求实数
是等差数列,求实数![]() 的值;
的值;
(3)在(2)的条件下,设![]() 记数列
记数列![]() 的前
的前![]() 项和为
项和为![]() ,若对任意的
,若对任意的![]() 存在实数
存在实数![]() ,使得
,使得![]() ,求实数
,求实数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】斐波那契数列,又称黄金分割数列.因数学家列昂纳多·斐波那契以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列:1、1、2、3、5、8、13、21、34、…..,在数学上,斐波那契数列以如下被递推的方法定义:![]() ,
,![]() ,
,![]() .这种递推方法适合研究生活中很多问题.比如:一六八中学食堂一楼到二楼有15个台阶,某同学一步可以跨一个或者两个台阶,则他到二楼就餐有( )种上楼方法.
.这种递推方法适合研究生活中很多问题.比如:一六八中学食堂一楼到二楼有15个台阶,某同学一步可以跨一个或者两个台阶,则他到二楼就餐有( )种上楼方法.
A.377B.610C.987D.1597
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学名著《九章算术》中有这样一个问題:今有牛、马、羊食人苗,苗主责之粟五斗,羊主曰:“我羊食半马、“马主曰:“我马食半牛,”今欲衰偿之,问各出几何?此问题的译文是:今有牛、马、羊吃了别人的禾苗,禾苗主人要求赔偿5斗粟、羊主人说:“我羊所吃的禾苗只有马的一半,”马主人说:“我马所吃的禾苗只有牛的一半,“打算按此比例偿还,他们各应偿还多少?该问题中,1斗为10升,则马主人应偿还( )升粟?
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A.命题“若![]() ,则
,则![]() ”的逆否命题为:“若
”的逆否命题为:“若![]() ,则
,则![]() ”
”
B.“![]() ”是“
”是“![]() ”的充分而不必要条件
”的充分而不必要条件
C.若![]() 且
且![]() 为假命题,则
为假命题,则![]() 、
、![]() 均为假命题
均为假命题
D.命题![]() “存在
“存在![]() ,使得
,使得![]() ”,则非
”,则非![]() “任意
“任意![]() ,均有
,均有![]() ”
”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业通过调查问卷(满分50分)的形式对本企业900名员工的工作满意程度进行调查,并随机抽取了其中30名员工(16名女工,14名男工)的得分,如下表:
女 | 47 | 36 | 32 | 48 | 34 | 44 | 43 | 47 | 46 | 41 | 43 | 42 | 50 | 43 | 35 | 49 |
男 | 37 | 35 | 34 | 43 | 46 | 36 | 38 | 40 | 39 | 32 | 48 | 33 | 40 | 34 |
(1)根据以上数据,估计该企业得分大于45分的员工人数;
(2)现用计算器求得这30名员工的平均得分为40.5分,若规定大于平局得分为 “满意”,否则为 “不满意”,请完成下列表格:
“满意”的人数 | “不满意”的人数 | 合计 | |
女员工 | 16 | ||
男员工 | 14 | ||
合计 | 30 |
(3)根据上述表中数据,利用独立性检验的方法判断,能否在犯错误的概率不超过1%的前提下,认为该企业员工“性别”与“工作是否满意”有关?
参考数据:
P(K2 | 0.10 | 0.050 | 0.025 | 0.010 | 0.001 |
K | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的焦点是
的焦点是![]() ,
,![]() 、
、![]() 是曲线
是曲线![]() 上不同两点,且存在实数
上不同两点,且存在实数![]() 使得
使得![]() ,曲线
,曲线![]() 在点
在点![]() 、
、![]() 处的两条切线相交于点
处的两条切线相交于点![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)点![]() 在
在![]() 轴上,以
轴上,以![]() 为直径的圆与
为直径的圆与![]() 的另一交点恰好是
的另一交点恰好是![]() 的中点,当
的中点,当![]() 时,求四边形
时,求四边形![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com