(理)已知圆(x+4)2+y2=25的圆心为M1,圆(x-4)2+y2=1的圆心为M2,一个动圆与这两个圆都外切.
(Ⅰ)求动圆圆心M的轨迹C的方程;
(Ⅱ)若经过点M2的直线与(Ⅰ)中的轨迹C有两个交点A、B,求|AM1|•|BM1|的最小值.
解:(I)∵动圆M与这两个圆都外切,
∴|MM
1|-5=|MM
2|-1
即|MM
1|-|MM
2|=4,
∵|MM
1|-|MM
2|=4,4<|M
1M
2|=8
∴动圆圆心M的轨迹是以M
1,M
2为焦点的双曲线的右支
由定义可得 c=4,a=2,b
2=12
∴动圆圆心M的轨迹C的方程为
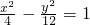
(x≥2)
(II)∵M
2(4,1),
∴设经过点M
2的直线方程为x=ty+4
代入双曲线方程
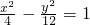
,并整理得(3t
2-1)y
2+24ty+36=0
设A(x
1,y
1),B(x
2,y
2),则有△>0,y
1+y
2=-

,y
1y
2=

由y
1y
2<0,得

而|AM
1|•|BM
1|=e(x
1+1)•e(x
2+1)=4(ty
1+5)(ty
2+5)
=4[t
2(y
1y
2)+5t(y
1+y
2)+25]
=4[t
2•

+5t•(-

)+25]
=-112×(1+

)+100
∵-1≤3t
2-1<0
∴当3t
2-1=-1时,即t=0时,|AM
1|•|BM
1|取得最小值100
分析:(I)利用定义法求动点M的轨迹方程,先利用圆与圆相切的几何条件,得到动点M满足的几何条件,再由曲线定义判断曲线形状,最后写出曲线的标准方程;(II)将经过点M
2的直线方程设为x=ty+4形式,代入(I)中的曲线,利用韦达定理和焦半径公式,将所求转化为关于t的函数,求其最小值即可
点评:本题考查了定义法求动点轨迹方程的方法,直线与双曲线的位置关系,韦达定理的应用及设而不求的解题技巧

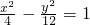 (x≥2)
(x≥2)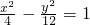 ,并整理得(3t2-1)y2+24ty+36=0
,并整理得(3t2-1)y2+24ty+36=0 ,y1y2=
,y1y2=

 +5t•(-
+5t•(- )+25]
)+25] )+100
)+100
